Complex Analysis/Goursat's Lemma (Details)

Goursat's Lemma, also known as the Goursat's Theorem, is a theorem in Complex Analysis. Goursat's lemma is a precursor to the Cauchy's integral theorem and is often used in its proof. It plays an important role in the development of complex analysis. Remarkably, the lemma only requires Complex differentiability but not continuous differentiability. The lemma was proved in its rectangular form by Édouard Goursat (1858–1936) and published in 1884. The triangular form commonly used today was introduced by Alfred Pringsheim.

Goursat's Lemma

Given the following assumptions:

(P1) Let ${U}\subseteq \mathbb {C}$ be an open subset,
(P2) Let ${z}_{1},{z}_{2},{z}_{3}\in \mathbb {C}$ be three non-collinear points that define the triangle

\Delta {\left({z}_{1},{z}_{2},{z}_{3}\right)}:=\left\{\sum _{k=1}^{3}\lambda _{k}\cdot {z}_{k}{\mid }{\left({\sum _{{k}{1}}^{3}}\lambda _{k}={1}\right)}\wedge \forall {k}\in {\left\lbrace {1},{2},{3}\right\rbrace }\lambda _{k}\in [{0},{1}]\right\}\subset {U}

(P3) Let ${f}:{U}\to \mathbb {C}$ be a holomorphic function,
(P4) Let ${\left\langle {z}_{1},{z}_{2},{z}_{3}\right\rangle }:{\left[{0},{3}\right]}\to \mathbb {C}$ be the closed path over the triangle edge of $\Delta {\left({z}_{1},{z}_{2},{z}_{3}\right)}$ with starting point ${z}_{1}$ ,

then the following statements hold:

(C1) $\int _{\left\langle {z}_{1},{z}_{2},{z}_{3}\right\rangle }{f{\left({z}\right)}}{d}{z}={0}$

Proof

Integration path along the triangle boundary

Subdivision of the outer paths and insertion of additional paths between the midpoints of the sides, which cancel out in the line integral due to the reversed direction of the integration path, resulting in a sum of 0 and leaving the total integral unchanged.

Inductive definition of the paths. The subtriangles are similar to the original triangle. By using the midpoints of the sides, the perimeter of a triangle

\Delta ^{(n)}

is halved with each step to

\Delta ^{(n+1)}

.

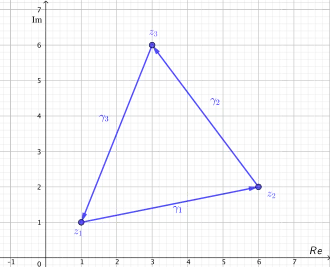
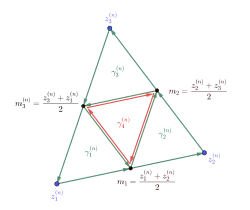
(S1) We define a sequence of triangular paths recursively as $\gamma ^{(n)}:={\left\langle z_{1}^{(n)},z_{2}^{(n)},z_{3}^{(n)}\right\rangle }$ .

Proof part 1: Definition of the triangle paths

(S2) (DEF) For ${n}={0}$ let the closed triangle path $\gamma ^{(0)}:[0,3]\to \mathbb {C}$ be defined as:

\gamma ^{(0)}(t):=\left\langle z_{1},z_{2},z_{3}\right\rangle (t):={\begin{cases}(1-t)\cdot z_{1}+t\cdot z_{2}&{\text{for }}t\in [0,1]\\(2-t)\cdot z_{2}+(t-1)\cdot z_{3}&{\text{for }}t\in (1,2]\\(3-t)\cdot z_{3}+(t-2)\cdot z_{1}&{\text{for }}t\in (2,3]\\\end{cases}}

Furthermore, let $\gamma ^{(n)}$ be already defined. We define $\gamma ^{(n+1)}$ inductively.

Justification: (P4,UT)

(S3) (DEF) Definition: Triangle path ${\gamma _{1}^{(n)}}:={\left\langle {\frac {z_{1}^{(n)}+z_{2}^{(n)}}{2}},z_{2}^{(n)},{\frac {z_{2}^{(n)}+z_{3}^{(n)}}{2}}\right\rangle }$ ,

Justification: (S3,S4,S5)

(S4) (DEF) Definition: Triangle path ${\gamma _{2}^{(n)}}:={\left\langle {\frac {z_{2}^{(n)}+z_{3}^{(n)}}{2}},z_{3}^{(n)},{\frac {z_{1}^{(n)}+z_{3}^{(n)}}{2}}\right\rangle }$ ,
(S5) (DEF) Definition: Triangle path ${\gamma _{3}^{(n)}}:={\left\langle {\frac {z_{1}^{(n)}+z_{3}^{(n)}}{2}},z_{1}^{(n)},{\frac {z_{1}^{(n)}+z_{2}^{(n)}}{2}}\right\rangle }$ ,
(S6) (DEF) Definition: Triangle path ${\gamma _{4}^{(n)}}:={\left\langle {\frac {z_{1}^{(n)}+z_{2}^{(n)}}{2}},{\frac {z_{2}^{(n)}+z_{3}^{(n)}}{2}},{\frac {z_{1}^{(n)}+z_{3}^{(n)}}{2}}\right\rangle }$
(S7) (DEF) Let ${i}\in {\left\lbrace {1},{2},{3},{4}\right\rbrace }$ be the smallest index with $\forall _{{k}\in {\left\lbrace {1},,{2},{3},{4}\right\rbrace }}:{\left|\int _{\gamma _{k}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}\leq {\left|\int _{\gamma _{i}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}$ and $\gamma ^{\left({n}+{1}\right)}:={\gamma _{i}^{(n)}}$

Proof part 2: Estimates

(S8) $\Rightarrow$ $\int _{\gamma ^{(n)}}f(z)\,dz=\sum _{k=1}^{4}\int _{\gamma _{k}}^{(n)}f(z)\,dz$
(S9) $\Rightarrow$ ${\left|\int _{\gamma ^{n}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}={\left|{\sum _{{k}={1}}^{4}}\int _{\gamma _{k}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}\leq {\sum _{{k}={1}}^{4}}{\left|\int _{\gamma _{k}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}\leq {4}\cdot {\left|\int _{\gamma _{k}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}$ for all ${n}\in \mathbb {N}$

Justification: (S7,WG4,DU)

(S10) $\Rightarrow$ ${0}\leq {\left|\int _{\left\langle {z}_{1},{z}_{2},{z}_{3}\right\rangle }{f{\left({z}\right)}}{d}{z}\right|}={\left|\int _{\gamma ^{(0)}}f(z){\left.{d}{z}\right.}\right|}\leq {4}\cdot {\left|\int _{\gamma ^{\left({1}\right)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}\leq \ldots \leq {4}^{n}\cdot {\left|\int _{\gamma _{i}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}={4}^{n}\cdot {\left|\int _{\gamma ^{\left({n}+{1}\right)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}$

Proof part 3: Diameter of the sub-triangles

(S11) The nested definition of the sub-triangles yields for all ${n}\in \mathbb {N}$ : $\Delta {\left({{z}_{1}^{(n)}},{{z}_{2}^{(n)}},{{z}_{3}^{(n)}}\right)}\supset \Delta {\left({{z}_{1}^{\left({n}+{1}\right)}},{{z}_{2}^{\left({n}+{1}\right)}},{{z}_{3}^{\left({n}+{1}\right)}}\right)}$ and

\lim _{n\to \infty }\,{\text{diam}}\left(\Delta {\left({{z}_{1}^{(n)}},{{z}_{2}^{(n)}},{{z}_{3}^{(n)}}\right)}\right)=0

(S12) $\Rightarrow$ $\exists _{{z}_{0}\in {U}}\forall _{{n}\in \mathbb {N} }:{z}_{0}\in \Delta ^{(n)}:=\Delta {\left({{z}_{1}^{(n)}},{{z}_{2}^{(n)}},{{z}_{3}^{(n)}}\right)}$ and ${\left\lbrace {z}_{0}\right\rbrace }=\bigcap _{{n}\in \mathbb {N} }\Delta ^{(n)}$

Proof part 4: Use of holomorphism (P3)

(S13) We use the holomorphism of $f$ in $z_{0}\in U$ for further steps with

f(z):=f(z_{0})+f'(z_{0})\cdot (z-z_{0})+r(z)

and

\lim _{z\to z_{0}}{\frac {r(z)}{z-z_{0}}}=0

Justification: (P3)

(S14) $\Rightarrow$ The function ${h}:{U}\to \mathbb {C}$ with $h(z):=f(z_{0})+f'(z_{0})\cdot (z-z_{0})$ has a primitive $H(z):=f(z_{0})+f'(z_{0})\cdot {\frac {1}{2}}\cdot (z-z_{0})^{2}$

Justification: since

h(z)

is a polynomial of degree 1.

(S15) $\Rightarrow$ The path integral over the closed paths $\gamma ^{(n)}$ of the function ${h}:{U}\to \mathbb {C}$ is thus $\int _{\gamma _{k}^{(n)}}{h}{\left({z}\right)}={0}$

Justification: (SF)

(S16) $\Rightarrow$ For the path integral over the closed paths $\gamma ^{(n)}$ of the function ${f}:{U}\to \mathbb {C}$ we have $\int _{\gamma _{k}^{(n)}}{f{{\left({z}\right)}{\left.{d}{z}\right.}}}=\int _{\gamma _{k}^{(n)}}{h}{\left({z}\right)}+{r}{\left({z}\right)}{\left.{d}{z}\right.}=\int _{\gamma _{k}^{(n)}}{r}{\left({z}\right)}{\left.{d}{z}\right.}$

Proof part 4: Estimate of the remainder term $r(z)$

(S17) $\Rightarrow$ With $\lim _{z\to z_{0}}{\frac {r(z)}{z-z_{0}}}=0$ we have: For all $\epsilon >{0}$ there exists a $\delta >{0}$

|z-z_{0}|<\delta \Rightarrow \left|{\frac {r(z)}{z-z_{0}}}\right|<\epsilon

Justification:

\epsilon

-

\delta

-criterion applied to

g(z):={\frac {r(z)}{z-z_{0}}}

and continuity of

g

in

z_{0}

(S18) $\Rightarrow$ For all $\epsilon >{0}$ there exists a $\delta >0$ : $|z-z_{0}|<\delta \Rightarrow |r(z)|<\epsilon \cdot |z-z_{0}|$

0\leq \left|\int _{\left\langle z_{1},z_{2},z_{3}\right\rangle }f(z)\,dz\right|\leq 4^{n}\cdot \left|\int _{\gamma _{k}^{(n)}}f(z)\,dz\right|=4^{n}\cdot \left|\int _{\gamma _{k}^{(n)}}r(z)\,dz\right|\leq 4^{n}\cdot \int _{\gamma _{k}^{(n)}}|r(z)|\,dz\leq 4^{n}\cdot \int _{\gamma _{k}^{(n)}}\epsilon \cdot |z-z_{0}|\,dz

Justification: (S2)

(S20) From the condition $\lim _{n\to \infty }{\text{diam}}\left(\Delta ^{(n)}\right)=0$ there exists for all $\epsilon >0$ an $n_{\delta }\in \mathbb {N}$ with $\Delta ^{(n)}\subseteq {D}_{\delta }(z_{0})$ for all $n>n_{\delta }$ .
(S21) $\Rightarrow$ $|z-z_{0}|<L\left(\gamma ^{(n)}\right)={\frac {1}{2^{n}}}\cdot L\left(\gamma \right)$ for all $n\in \mathbb {N}$ and all $z\in \Delta ^{(n)}$

Justification: The factor

{\frac {1}{2^{n}}}

arises from the continued halving of the sides of the triangles

\Delta ^{(n)}

(S22) This implies:

0\leq \left|\int _{\langle z_{1},z_{2},z_{3}\rangle }f(z)\,dz\right|\leq 4^{n}\cdot \int _{\gamma _{k}^{(n)}}\epsilon \cdot |z-z_{0}|\,dz\leq 4^{n}\cdot \epsilon \cdot \int _{\gamma _{k}^{(n)}}{\frac {1}{2^{n}}}\cdot {\mathcal {L}}(\gamma )\,dz=4^{n}\cdot \epsilon \cdot {\frac {1}{2^{n}}}\cdot {\mathcal {L}}(\gamma )\underbrace {\leq \int _{\gamma _{k}^{(n)}}1\,dz} _{{\mathcal {L}}(\gamma _{k}^{(n)})}

\leq 4^{n}\cdot \epsilon \cdot {\frac {1}{2^{n}}}\cdot L(\gamma )\cdot {\mathcal {L}}(\gamma _{k}^{(n)})\leq 4^{n}\cdot \epsilon \cdot {\frac {{\mathcal {L}}(\gamma )}{4^{n}}}=\epsilon \cdot {\mathcal {L}}(\gamma )

for all

\epsilon >0

Justification: (S19,LIW,IAL)

(C1) $\Rightarrow$ $\int _{\left\langle {z}_{1},{z}_{2},{z}_{3}\right\rangle }{f{\left({z}\right)}}{d}{z}={0}$

Abbreviations for justifications

(DU) $\forall _{a,b\in \mathbb {C} }:|a+b|\leq |a|+|b|$
(DI) Definition: Let $M\subset {C}$ be a set ${\text{diam}}(M):={\text{sup}}\lbrace |b-a|\,:\,a,b\in M\rbrace$
(WE) Definition (Path): Let ${U}\subseteq \mathbb {C}$ be a subset and $a,b\in \mathbb {R}$ with $a<b$ . A path $\gamma$ in $U\subseteq \mathbb {C}$ is a continuous mapping ${\displaystyle \gamma$ .
(SPU) Definition (Trace): Let ${\displaystyle \gamma$ be a path in ${U}\subseteq \mathbb {C}$ . The trace of $\gamma$ is defined as: ${\text{Spur}}(\gamma ):=\lbrace \gamma (t)\in \mathbb {C} \,{\mid }\,t\in [a,b]\rbrace$ .
(WZ) Definition (Path-connected): Let ${U}\subseteq \mathbb {C}$ be a subset. ${U}$ is called path-connected if there exists a path ${\displaystyle \gamma$ in $U\subseteq \mathbb {C}$ with $\gamma (a)=z_{1}$ , $\gamma (b)=z_{2}$ and ${\text{Spur}}(\gamma )\subseteq U$ .
(GE) Definition (Domain): A subset ${G}\subseteq \mathbb {C}$ is called a domain if (1) ${G}$ is open, (2) ${G}\neq \emptyset$ and (3) ${G}$ is path-connected.
(WG1) Definition (Smooth path): A path ${\displaystyle \gamma$ is smooth if it is continuously differentiable.
(UT) Definition (Subdivision): Let $[a,b]$ be an interval, $n\in \mathbb {N}$ and ${a}={u}_{0}<{\ldots }<{u}_{n}={b}$ . ${\left({u}_{0},\ldots ,{u}_{n}\right)}\in \mathbb {R} ^{n+1}$ is called a subdivision of ${\left[{a},{b}\right]}$ .
(WG2) Definition (Path subdivision): Let ${\displaystyle \gamma$ be a path in ${U}\subseteq \mathbb {C}$ , ${n}\in \mathbb {N}$ , ${\left({u}_{0},\ldots ,{u}_{n}\right)}$ a subdivision of $[a,b]$ , $\gamma _{k}:{\left[{u}_{{k}-{1}},{u}_{k}\right]}\to \mathbb {C}$ for all ${k}\in {\left\lbrace {1},\ldots ,{n}\right\rbrace }$ a path in ${U}$ . ${\left(\gamma _{1},\ldots ,\gamma _{n}\right)}$ is called a path subdivision of $\gamma$ if $\gamma _{n}{\left({b}\right)}=\gamma {\left({b}\right)}$ and $\forall _{{k}\in {\left\lbrace {1},\ldots ,{n}\right\rbrace }}\forall _{{t}\in {\left[{u}_{{k}-{1}},{u}_{k}\right)}}:\gamma _{k}{\left({t}\right)}=\gamma {\left({t}\right)}\wedge \gamma _{k}{\left({u}_{{k}-{1}}\right)}=\gamma _{{k}-{1}}{\left({u}_{k}\right)}$ .
(WG3) Definition (Piecewise smooth path): A path ${\displaystyle \gamma$ is piecewise smooth if there exists a path subdivision ${\left(\gamma _{1},\ldots \gamma _{n}\right)}$ of $\gamma$ consisting of smooth paths $\gamma _{k}$ for all ${k}\in {\left\lbrace {1},\ldots ,{n}\right\rbrace }$ .
(WG4) Definition (Path integral): Let $f:U\to \mathbb {C}$ be a continuous function and ${\displaystyle \gamma$ a smooth path, then the path integral is defined as: $\int _{\gamma }f:=\int _{\gamma }f(z)\,dz:=\int _{a}^{b}f(\gamma (t))\cdot \gamma '(t)\,dt$ . If $\gamma$ is only piecewise smooth with respect to a path subdivision $(\gamma _{1},\ldots ,\gamma _{n})$ , then we define $\int _{\gamma }f(z)\,dz:=\sum _{k=1}^{n}\int _{\gamma _{k}}f(z)\,dz$ .
(SF) Theorem (Primitive with closed paths): If a continuous function $f:U\to \mathbb {C}$ has a primitive $F:U\to \mathbb {C}$ , then for a piecewise smooth path ${\displaystyle \gamma$ we have $\int _{\gamma }f(z)\,dz=F(b)-F(a)$ .
(LIW) Length of the integration path: Let ${\displaystyle \gamma$ be a smooth path, then the ${\mathcal {L}}(\gamma )$ is defined as:

{\mathcal {L}}(\gamma ):=\int _{a}^{b}|\gamma '(t)|\,dt

.

If

{\displaystyle \gamma

is a general integration path with the path subdivision

{\left(\gamma _{1},\ldots \gamma _{n}\right)}

of smooth paths

\gamma _{k}

, then

{\mathcal {L}}(\gamma )

is defined as the sum of the lengths of the smooth paths

\gamma _{k}

, i.e.:

{\mathcal {L}}(\gamma ):=\sum _{k=1}^{n}{\mathcal {L}}(\gamma _{k})

(IAL) Integral estimate over the length of the integration path: Let ${\displaystyle \gamma$ be an integration path on the domain $G\subseteq \mathbb {C}$ , then for a continuous function $f$ on ${\text{Spur}}(\gamma )$ we have the estimate:

\left|\int _{\gamma }f(z)\,dz\right|\leq \max _{z\in {\text{Spur}}(\gamma )}|f(z)|\cdot {\mathcal {L}}(\gamma )

Literature

Eberhard Freitag & Rolf Busam: Funktionentheorie 1, Springer-Verlag, Berlin

Page Information

You can display this page as Wiki2Reveal slides

Wiki2Reveal

The Wiki2Reveal slides were created for the Complex Analysis' and the Link for the Wiki2Reveal Slides was created with the link generator.

This page is designed as a PanDocElectron-SLIDE document type.
Source: Wikiversity https://en.wikiversity.org/wiki/Complex%20Analysis/Goursat's%20Lemma%20(Details)
see Wiki2Reveal for the functionality of Wiki2Reveal.

Translation and Version Control

This page was translated based on the following Wikiversity source page and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:

Source: Lemma von Goursat (Details) - URL: https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Lemma_von_Goursat_(Details)
Date: 11/13/2024

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.