Complex Analysis/Paths

Definition: Path

Let ${\displaystyle U\subset \mathbb {C} }$ be a subset. A path in ${\displaystyle U}$ is a continuous mapping with:

${\displaystyle \gamma \colon [a,b]\rightarrow U}$ with ${\displaystyle a<b}$ and ${\displaystyle a,b\in \mathbb {R} }$.

Definition: Trace of a Path

The trace of a path ${\displaystyle \gamma \colon [a,b]\rightarrow U}$ in ${\displaystyle U\subset \mathbb {C} }$ is the image or range of the function ${\displaystyle \gamma }$:

${\displaystyle \mathrm {Trace} (\gamma ):={\gamma (t)\in \mathbb {C} \ |\ t\in [a,b]}}$

Definition: Closed Path

Let ${\displaystyle \gamma \colon [a,b]\rightarrow U}$ be a path in ${\displaystyle U\subset \mathbb {C} }$. The mapping ${\displaystyle \gamma }$ is called a closed path if:

${\displaystyle \gamma (a)=\gamma (b)}$

Definition: Region

Let ${\displaystyle U\subset \mathbb {C} }$ be an open subset of ${\displaystyle \mathbb {C} }$. Then ${\displaystyle U}$ is called a region.

Definition: Path-Connected

Let ${\displaystyle U\subset \mathbb {C} }$ be a non-empty set.

${\displaystyle U}$ is path-connected ${\displaystyle$ :\Longleftrightarrow \ \forall _{z_{1},z_{2}\in U}\exists _{\gamma \colon [a,b]\rightarrow U}:\ \gamma (a)=z_{1}\wedge \gamma (b)=z_{2}\wedge {Spur}(\gamma )\subseteq U}

Definition: Domain

Let ${\displaystyle G\subset \mathbb {C} }$ be a non-empty subset of ${\displaystyle \mathbb {C} }$. If

• ${\displaystyle G}$ is open
• ${\displaystyle G}$ is path-connected

Then ${\displaystyle G}$ is called a domain in ${\displaystyle \mathbb {C} }$.

Example (Circular Paths)

Let ${\displaystyle z_{o}\in \mathbb {C} }$ be a complex number, and let ${\displaystyle r>0}$ be a radius. A circular path ${\displaystyle \gamma _{z_{o},r}\colon [0,2\pi ]\rightarrow \mathbb {C} }$ around ${\displaystyle z_{o}\in \mathbb {C} }$ is defined as:

${\displaystyle \gamma _{z_{o},r}(t):=z_{o}+r\cdot e^{i\cdot t}}$

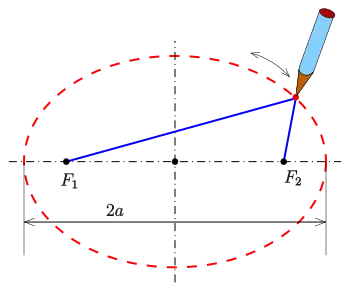
Example - Paths with Ellipse as Trace

Let ${\displaystyle z_{o}\in \mathbb {C} }$ be a complex number, and let ${\displaystyle a,b>0}$ be the semi-axes of an ellipse. An elliptical path ${\displaystyle \gamma _{z_{o},a,b}\colon [0,2\pi ]\rightarrow \mathbb {C} }$ around ${\displaystyle z_{o}\in \mathbb {C} }$ is defined as:

${\displaystyle \gamma _{z_{o},a,b}(t):=z_{o}+a\cdot \cos(t)+i\cdot b\cdot \sin(t)}$

Gardener's Construction of an Ellipse

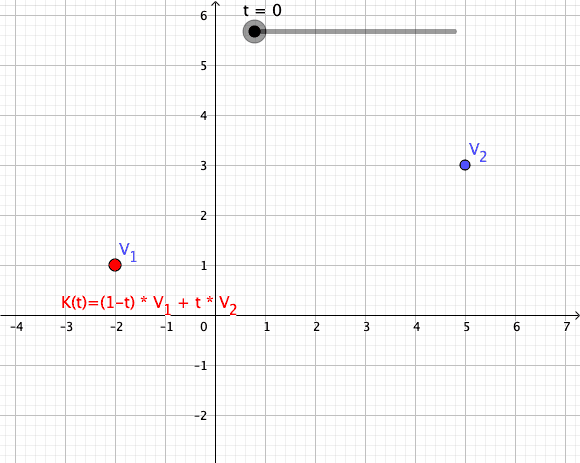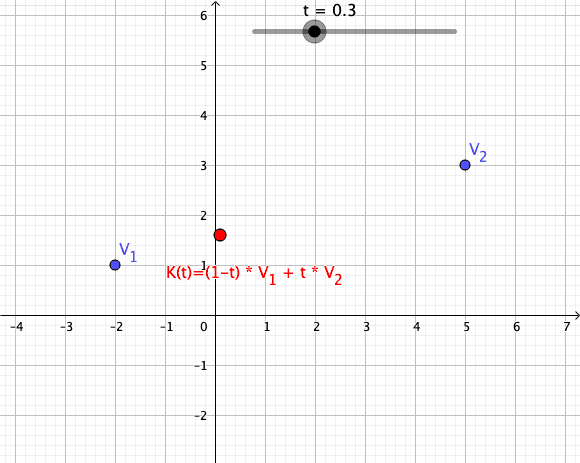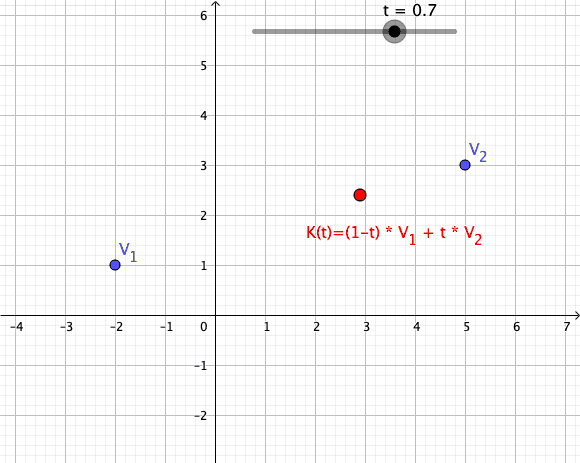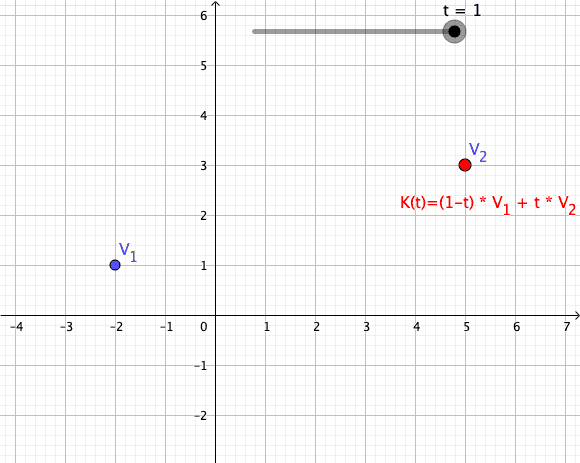
Convex Combinations

Let ${\displaystyle z_{1},z_{2}\in \mathbb {C} }$ be complex numbers, and let ${\displaystyle t\in [0,1]}$ be a scalar. A path ${\displaystyle \gamma _{z_{1},z_{2}}\colon [0,1]\rightarrow \mathbb {C} }$ is defined such that its trace is the line segment connecting ${\displaystyle z_{1},z_{2}\in \mathbb {C} }$:

${\displaystyle \gamma _{z_{1},z2}(t):=(1-t)\cdot z_{1}+t\cdot z_{2}}$

Such a path is called a convex combination of the first order (see also Convex Combinations of higher order).

Animation of a Convex Combination of Two Vectors as Mapping

Convex Combination as Mapping in an Animated GIF

Integration Path

Let ${\displaystyle G\subset \mathbb {C} }$ be a domain. An integration path in ${\displaystyle G}$ is a path that is piecewise continuously differentiable with

${\displaystyle \gamma \colon [a,b]\rightarrow U}$ with ${\displaystyle a<b}$ and ${\displaystyle a,b\in \mathbb {R} }$.

See Also

• Ellipse
• Convex Combination
• Topological vector space

Page Information

You can display this page as Wiki2Reveal slides