Complex Analysis/Power series

Introduction

This page about Power series for the course Complex Analysis can be displayed as Wiki2Reveal slides. Single sections are regarded as slides and modifications on the slides will immediately affect the content of the slides. The following aspects of Power series are considered in detail:

(1) Definition of power series,
(2) Radius of convergence
(3) Taylor series

Definition

Power series ${\textstyle p(x)}$ is in Calculus a series of the following form

p(x)=\sum _{n=0}^{\infty }p_{n}(x-x_{0})^{n}

with

any sequence ${\textstyle (p_{n})_{n\in \mathbb {N} _{0}}}$ real or complex number
the 'center of series' is ${\textstyle x_{0}}$ .

Reference to real analysis

Potency series play an important role in the Complex Analysis and often allow a meaningful continuation real function into the complex numerical level. In particular, the question arises for which real or complex numbers converge a potency series. This question leads to the term radius of convergence.

Convergence radius

The largest number ${\textstyle x_{0}}$ is defined as the convergence radius of a potency series around the development point ${\textstyle r}$ , for which the potency series for all ${\textstyle x}$ with ${\textstyle r>|x-x_{0}|}$ The open ball ${\textstyle U_{r}(x_{0})}$ with radius ${\textstyle r}$ around ${\textstyle x_{0}}$ are called 'convergence circle'. The convergence radius is therefore the radius of the convergence circle. If the series is converged for all ${\textstyle x}$ , it is said that the convergence radius is infinite. Converged only for ${\textstyle x_{0}}$ , the convergence radius is 0, the row is then sometimes called 'nowhere convergent.

Calculation Convergence radius - Cauchy-Hadamard

For power series, the convergence radius ${\textstyle r}$ can be calculated with the 'formula of Cauchy-Hadamard'. It shall apply:

r={\frac {1}{\limsup \limits _{n\rightarrow \infty }\ {\sqrt[{n}]{|a_{n}|}}}}

In this context, ${\textstyle {\tfrac {1}{0}}:=+\infty }$ and ${\textstyle {\tfrac {1}{\infty }}:=0}$ are defined

Calculation Convergence radius - non-threatening coefficients

In many cases, the convergence radius can also be calculated in a simpler manner in the case of potency rows with non-shrinkable coefficients. In fact,

r=\lim _{n\to \infty }\left|{\frac {a_{n}}{a_{n+1}}}\right|,

where this limit value exists.

Examples

Each Polynomial function can be classified as a power series, in which almost all coefficients ${\textstyle a_{n}}$ are equal to 0. Important other examples are Taylor series and Maclaurin series. Functions which can be represented by a power series are also called analytical Function. Here again by way of example the potency series representation of some known functions:

Exponential function

Exponential function ${\textstyle exp:\mathbb {C} \to \mathbb {C} \setminus \{0\}}$ :

e^{z}=\exp(z)=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}={\frac {z^{0}}{0!}}+{\frac {z^{1}}{1!}}+{\frac {z^{2}}{2!}}+{\frac {z^{3}}{3!}}+\dotsb

for all ${\textstyle x\in \mathbb {C} }$ , i.e., the convergence radius is infinite.

Sinus function/cosine

Sinus:

\sin(x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n+1}}{(2n+1)!}}={\frac {x}{1!}}-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}\mp \dotsb

Kosinus:

\cos(x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n}}{(2n)!}}={\frac {x^{0}}{0!}}-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}\mp \dotsb

Convergence radius for sin, cos, exp

The radius of convergence is infinite both for the sine, cosine and for the exponential function. The potency series representation results directly from the exponential function with the Euler's formula.

Animation of Approximation with Taylor polynomial

The following animation shows the approximation of $cos(z)$ with Taylor polynomials with an increasing degree.

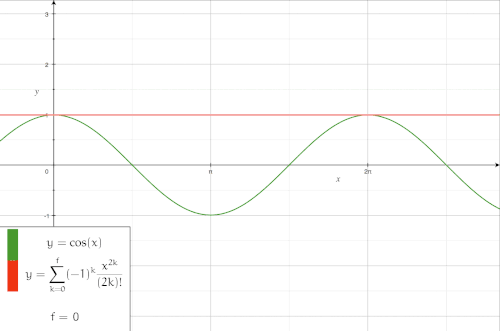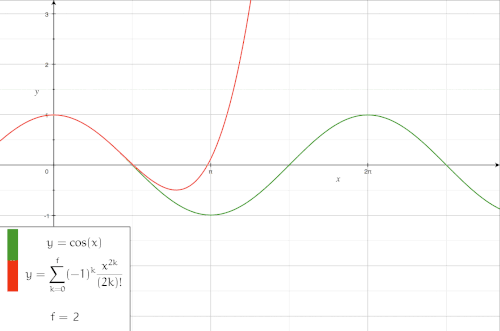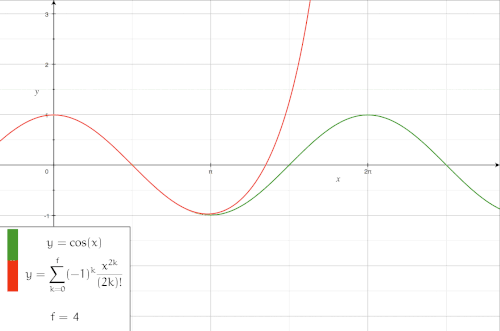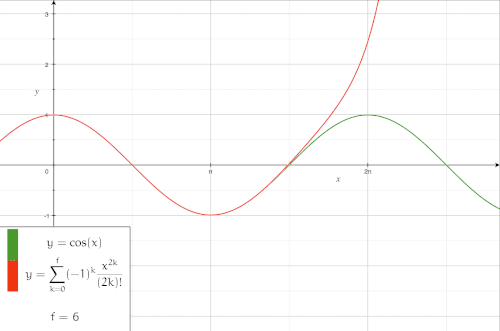
Approximation of cos(z) with a Taylor sum as animation

Logarithm

Logarithm function:

\ln(1+z)=\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {z^{k}}{k}}=z-{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}-{\frac {z^{4}}{4}}+\dotsb

for ${\textstyle |z|<1}$ , i.e. The convergence radius is 1, for ${\textstyle z=1}$ the series is convergent, for ${\textstyle z=-1}$ divergent.

Root

root function:

{\sqrt {1+x}}=1+{\frac {1}{2}}x-{\frac {1}{2\cdot 4}}x^{2}+{\frac {1\cdot 3}{2\cdot 4\cdot 6}}x^{3}\mp \dotsb

for ${\textstyle -1\leq x\leq 1}$ , i.e., the convergence radius in ${\textstyle \mathbb {R} }$ is 1 and the series converged both for ${\textstyle x=1}$ and for ${\textstyle x=-1}$ .

Characteristics

The power series is important in the function theory because holomorphic functions can always be developed locally in potency rows. The following topics are dealt with in the course.

Continuity - Differentiability

Power series are normal convergent within their circle of convergent. This directly follows that each function defined by a power series is continuous. Furthermore, it follows that there uniform convergence on compact subsets of the circle of convergence. This justifies the term-by-term differentiation and integration of a power series and shows that power series are infinitely differentiable.

Absolute convergence

Absolute convergence exists within the circle of convergence. No general statement can be made about the behaviour of a potency series on the edge of the convergence circle, but in some cases the Abel limit theorem allows to make a statement.

Uniqueness of the power series representation

The power series representation of a function around a development point is clearly determined (identity set for potency rows). In particular, for a given development point, Taylor development is the only possible potency series development.

Operations with potency series

Potency rows ${\textstyle p}$ can be recorded as vectors in a vector space ${\textstyle (\mathbb {C} [z],+,\cdot ,\mathbb {C} )}$ .

Addition and scalar multiplication

Are ${\textstyle f}$ and ${\textstyle g}$ by two potency rows

f(x)=\sum _{n=0}^{\infty }a_{n}(x-x_{0})^{n}

g(x)=\sum _{n=0}^{\infty }b_{n}(x-x_{0})^{n}

with the convergence radius ${\textstyle r}$ .

Scale multiplication

If ${\textstyle f}$ and ${\textstyle g}$ are due to two potency rows and ${\textstyle c}$ is a fixed complex number, then ${\textstyle f+g}$ and ${\textstyle cf}$ are considered to be at least

f(x)+g(x)=\sum _{n=0}^{\infty }(a_{n}+b_{n})(x-x_{0})^{n}

cf(x)=\sum _{n=0}^{\infty }(ca_{n})(x-x_{0})^{n}

Multiplication

The product of two potency rows with the convergence radius ${\textstyle r}$ is a potency row with a convergence radius which is at least ${\textstyle r}$ . Since there is absolute convergence within the convergence circle, the following applies after Cauchy-Product formula:

{\begin{aligned}f(x)g(x)&=\left(\sum _{n=0}^{\infty }a_{n}(x-x_{0})^{n}\right)\left(\sum _{n=0}^{\infty }b_{n}(x-x_{0})^{n}\right)\\&=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }a_{i}b_{j}(x-x_{0})^{i+j}=\sum _{n=0}^{\infty }\left(\sum _{i=0}^{n}a_{i}b_{n-i}\right)(x-x_{0})^{n}\end{aligned}}

The sequence defined by ${\textstyle \textstyle c_{n}=\sum _{i=0}^{n}a_{i}b_{n-i}}$ ${\textstyle (c_{n})}$ is called Faltung or convolution of the two sequences ${\textstyle (a_{n})}$ and ${\textstyle (b_{n})}$ .

Chain

There were ${\textstyle f}$ and ${\textstyle g}$ two potency series

f(x)=\sum _{n=0}^{\infty }a_{n}(x-x_{1})^{n}.{\mbox{.und }}g(x)=\sum _{n=0}^{\infty }b_{n}(x-x_{0})^{n}

with positive convergence radii and property

b_{0}=g(x_{0})=x_{1}

.

The linking ${\textstyle f\circ g}$ of both functions can then be developed locally again analytical Function and thus by ${\textstyle x_{0}}$ into a potency series:

(f\circ g)(x)=\sum _{n=0}^{\infty }c_{n}(x-x_{0})^{n}

Taylor series

According to Taylor's theorem:

c_{n}={\frac {(f\circ g)^{(n)}(x_{0})}{n!}}

With the Formel von Faà di Bruno, this expression can now be indicated in a closed formula as a function of the given series coefficients, since:

{\begin{aligned}f^{(n)}(g(x_{0}))&=f^{(n)}(x_{1})\\&=n!\cdot a_{n}\\g^{(m)}(x_{0})&=m!\cdot b_{m}\end{aligned}}

Multiindex procedure is obtained:

{\begin{aligned}c_{n}&={\frac {(f\circ g)^{(n)}(x_{0})}{n!}}\\&=\sum _{{\boldsymbol {k}}\in T_{n}}{\frac {f^{(|{\boldsymbol {k}}|)}(g(x_{0}))}{{\boldsymbol {k}}!}}\prod _{m=1 \atop k_{m}\geq 1}^{n}\left({\frac {g^{(m)}(x_{0})}{m!}}\right)^{k_{m}}\\&=\sum _{{\boldsymbol {k}}\in T_{n}}{\frac {|{\boldsymbol {k}}|!\cdot a_{|{\boldsymbol {k}}|}}{{\boldsymbol {k}}!}}\prod _{m=1 \atop k_{m}\geq 1}^{n}b_{m}^{k_{m}}\\&=\sum _{{\boldsymbol {k}}\in T_{n}}{{|{\boldsymbol {k}}|} \choose {\boldsymbol {k}}}\,a_{|{\boldsymbol {k}}|}\prod _{m=1 \atop k_{m}\geq 1}^{n}b_{m}^{k_{m}}\end{aligned}}

${\textstyle {{|{\boldsymbol {k}}|} \choose {\boldsymbol {k}}}}$ of the Multinomial coeffizient is ${\textstyle {\boldsymbol {k}}}$ and ${\textstyle T_{n}=\left\{{\boldsymbol {k}}\in \mathbb {N} _{0}^{n}\,{\Big |}\,\sum _{j=1}^{n}j\cdot k_{j}=n\right\}}$ is the amount of all partitions of ${\textstyle n}$ (cf.

Differentiation and integration

A potency series can be differentiated in the interior of its convergence circle and the derivative is obtained by elemental differentiation:

f^{\prime }(x)=\sum _{n=1}^{\infty }a_{n}n\left(x-x_{0}\right)^{n-1}=\sum _{n=0}^{\infty }a_{n+1}\left(n+1\right)\left(x-x_{0}\right)^{n}

${\textstyle f}$ can be differentiated as often as desired and the following applies:

f^{(k)}(x)=\sum _{n=k}^{\infty }{\frac {n!}{(n-k)!}}a_{n}(x-x_{0})^{n-k}=\sum _{n=0}^{\infty }{\frac {(n+k)!}{n!}}a_{n+k}(x-x_{0})^{n}

Analogously, a antiderivative is obtained by means of a link-wise integration of a potency series:

\int f(x)\,{\text{d}}x=\sum _{n=0}^{\infty }{\frac {a_{n}\left(x-x_{0}\right)^{n+1}}{n+1}}+C=\sum _{n=1}^{\infty }{\frac {a_{n-1}\left(x-x_{0}\right)^{n}}{n}}+C

In both cases, the convergence radius is equal to that of the original row.

Presentation of functions as potency series

Often, a given function is interested in a potency series representation – in particular to answer the question whether the function analytic is. There are some strategies to determine a potential series representation, the most common by the Taylor series. Here, however, the problem often arises that one needs a closed representation for the discharges, which is often difficult to determine. However, there are some lighter strategies for fuctional rational functions. As an example the function

f(z)={\frac {z^{2}}{z^{2}-4z+3}}

to be considered.

By means of the geometric series

By factoring the denominator and subsequent use of the formula for the sum of a geometrischen Reihe, a representation of the function as a product of infinite rows is obtained:

f(z)={\frac {z^{2}}{(1-z)(3-z)}}={\frac {z^{2}}{3}}\cdot {\frac {1}{1-z}}\cdot {\frac {1}{1-{\frac {z}{3}}}}=

={\frac {z^{2}}{3}}\cdot \left(\sum _{n=0}^{\infty }z^{n}\right)\cdot \left(\sum _{n=0}^{\infty }\left({\frac {z}{3}}\right)^{n}\right)={\frac {1}{3}}\left(\sum _{n=2}^{\infty }z^{n}\right)\left(\sum _{n=0}^{\infty }\left({\frac {z}{3}}\right)^{n}\right)

Product of geometric rows

Both rows are potency rows around the development point ${\textstyle z_{0}=0}$ and can therefore be multiplied in the above-mentioned manner. The same result also provides the Cauchy-Product formula

f(z)=\sum _{n=0}^{\infty }\left(\underbrace {\sum _{k=0}^{n}a_{k}b_{n-k}} _{c_{n}}\right)\cdot z^{n}

Series (mathematics)

Coefficients of individual series

The following shall apply:

a_{k}={\begin{cases}0&{\text{ für }}k\in \{0,1\}\\1&{\text{ sonst}}\end{cases}}

and

b_{k}={\frac {1}{3^{k}}}.

Cauchy product formula

This follows by applying the formula for the partial sum of a geometric series

c_{n}=\sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=2}^{n}\left({\frac {1}{3}}\right)^{n-k}={\frac {1}{3^{n-2}}}\sum _{k=0}^{n-2}3^{k}=-{\frac {1-3^{n-1}}{2\cdot 3^{n-2}}}

as a closed representation for the coefficient sequence of the potency series. Thus, the potency series representation of the function around the development point 0 is given by

f(z)=\sum _{n=2}^{\infty }{\frac {3}{2}}\cdot \left(1-{\frac {1}{3^{n-1}}}\right)\cdot z^{n}

.

Application of geometric rows or coefficient comparison

As an alternative to geometrical series, it is an alternative to coefficient comparison is an alternative: One assumes that a power series representation exists for ${\textstyle f}$ :

f(z)={\frac {z^{2}}{z^{2}-4z+3}}=\sum _{n=0}^{\infty }c_{n}z^{n}

The function ${\textstyle f}$ has the unknown coefficient sequence ${\textstyle (c_{n})_{n\in \mathbb {N} }}$ . After multiplication of the denominator and an index shift, the identity results:

{\begin{aligned}z^{2}&=(z^{2}-4z+3)\sum _{n=0}^{\infty }c_{n}z^{n}\\&=\sum _{n=2}^{\infty }c_{n-2}z^{n}-\sum _{n=1}^{\infty }4c_{n-1}z^{n}+\sum _{n=0}^{\infty }3c_{n}z^{n}\\&=3c_{0}+z(3c_{1}-4c_{0})+\sum _{n=2}^{\infty }(c_{n-2}-4c_{n-1}+3c_{n})z^{n}\end{aligned}}

The potency series ${\textstyle g(z):=z^{2}Series(mathematics)}$ is compared with the potency series ${\textstyle h(z):=3c_{0}+z(3c_{1}-4c_{0})+\sum _{n=2}^{\infty }(c_{n-2}-4c_{n-1}+3c_{n})z^{n}}$ . Both potency rows have the same development point ${\textstyle z_{o}=0}$ . Therefore, the coefficients of both potency rows must also correspond. Thus, the coefficient of (698-1047-1731592552598-341-99 must be ${\textstyle 0=3c_{0}}$ , for which the coefficient of ${\textstyle z^{1}}$ applies ${\textstyle 0=3c_{1}-4c_{0}}$ , ...

Recursion formula for coefficients

However, since two potency rows are exactly the same when their coefficient sequences correspond, the coefficient comparison results

c_{0}=0,\ c_{1}=0,\ c_{2}={\frac {1}{3}}

and the recursion equation

r=\lim _{n\to \infty }\left|{\frac {a_{n}}{a_{n+1}}}\right|,

;

the above closed representation follows from the complete induction.

Benefits coefficient comparison

The method by means of coefficient comparison also has the advantage that other development points than ${\textstyle z_{0}=0}$ are possible. Consider the development point ${\textstyle z_{1}=-1}$ as an example. First, the broken rational function must be shown as a polynomial in ${\textstyle (z-z_{1})=(z+1)}$ :

f(z)={\frac {z^{2}}{z^{2}-4z+3}}={\frac {(z+1)^{2}-2(z+1)+1}{(z+1)^{2}-6(z+1)+8}}

Other points of development

Analogously to the top, it is now assumed that a formal potency series around the development point exists with unknown coefficient sequence and multiplied by the denominator:

{\begin{aligned}(z+1)^{2}-2(z+1)+1&=((z+1)^{2}-6(z+1)+8)\sum _{n=0}^{\infty }c_{n}(z+1)^{n}\\&=8c_{0}+(z+1)(8c_{1}-6c_{0})+\\&\qquad +\sum _{n=2}^{\infty }(c_{n-2}-6c_{n-1}+8c_{n})(z+1)^{n}\end{aligned}}

Again, by means of coefficient comparison

c_{0}={\frac {1}{8}},\ c_{1}=-{\frac {5}{32}},\ c_{2}=-{\frac {1}{128}}

and as a recursion equation for the coefficients:

c_{n}={\frac {-c_{n-2}+6c_{n-1}}{8}}

Partial fraction decomposition

If the given function is first applied Polynomial division and then Partial fraction decomposition, the representation is obtained

f(z)={\frac {z^{2}}{z^{2}-4z+3}}=1+{\frac {4z-3}{(z-1)(z-3)}}=1+{\frac {1}{2}}\cdot {\frac {1}{1-z}}-{\frac {3}{2}}\cdot {\frac {1}{1-{\frac {z}{3}}}}

.

By inserting the geometric row, the following results:

{f(z)=1+{\frac {1}{2}}\cdot \sum _{n=0}^{\infty }z^{n}-{\frac {3}{2}}\cdot \sum _{n=0}^{\infty }{\frac {1}{3^{n}}}z^{n}=1+\sum _{n=0}^{\infty }{\frac {3}{2}}\cdot \left(1-{\frac {1}{3^{n-1}}}\right)z^{n}}

The first three sequence elements of the coefficient sequence are all zero, and the representation given here agrees with the upper one.

Generalizations

Potency rows can be defined not only for ${\textstyle x\in \mathbb {R} }$ , but are also generalizable. Thus, for example, R B is the Matrix exponential and the Matrix logarithm generalizations of potency rows in the area of the square of matrices. If in a row also potencies with negative integer exponents occur, one speaks of a Laurent-series. If the exponent is allowed to accept broken values Series (mathematics), it is a Puiseux-series. Formal power series are used, for example, as generating Functions in combinations and probabilitytheoery (for example probability generating functions). In the Algebra, formal power series are examined over general complex ring.

References

Kurt Endl, Wolfgang Luh: Analysis II.' Aula-Verlag 1973, 7th edition 1989, ISBN 3-89104-455-0, pp. 85–89, 99.
E. D. Solomentsev: Power series. In: Encyclopedia of Mathematics

Page Information

You can display this page as Wiki2Reveal slides

Wiki2Reveal

The Wiki2Reveal slides were created for the Complex Analysis' and the Link for the Wiki2Reveal Slides was created with the link generator.

This page is designed as a PanDocElectron-SLIDE document type.
Source: Wikiversity https://en.wikiversity.org/wiki/Complex%20Analysis/Power%20series
see Wiki2Reveal for the functionality of Wiki2Reveal.

Translation and Version Control

This page was translated based on the following Wikiversity source page and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.