Complex Analysis/Sequences and series

Notation

For the limit value ${\textstyle a_{0}\in \mathbb {C} }$ of a sequence ${\textstyle (a_{n})_{n\in \mathbb {N} }\in \mathbb {C} ^{\mathbb {N} }}$ there is a separate symbol, you write:

${\textstyle \lim _{n\to \infty }a_{n}=a_{0}}$ with ${\textstyle n\in \mathbb {N} }$.

Definition sequence convergence

Be ${\textstyle (a_{n})_{n\in \mathbb {N} }\in \mathbb {C} ^{\mathbb {N} }}$ a complex number sequence and ${\textstyle a_{0}\in \mathbb {C} }$. The convergence of ${\textstyle (a_{n})_{n\in \mathbb {N} }}$ against ${\textstyle a_{0}}$ is then defined as follows:

$${\displaystyle \lim _{n\to \infty }a_{n}=a_{0}\quad$$ :\Longleftrightarrow \quad \forall \varepsilon >0\;\exists n_{\varepsilon }\in \mathbb {N} \;\forall n\geq n_{\varepsilon }:\;\left|a_{n}-a_{0}\right|<\varepsilon } .

Notation

In addition to the notation above, we can denote

• ${\textstyle a_{n}\to a_{0}}$ for ${\textstyle n\to \infty }$ or
• just ${\displaystyle a_{n}\to a_{0}\in \mathbb {C} }$ resp. ${\displaystyle a_{n}{}_{\stackrel {\displaystyle \longrightarrow }{n\to \infty }}a_{0}\in \mathbb {C} }$ can be used.

Visualization of convergence

Epsilon Environment and convergence

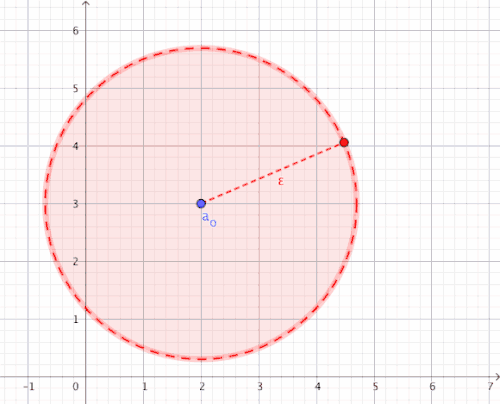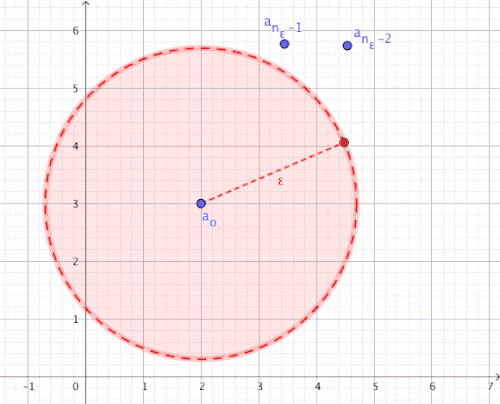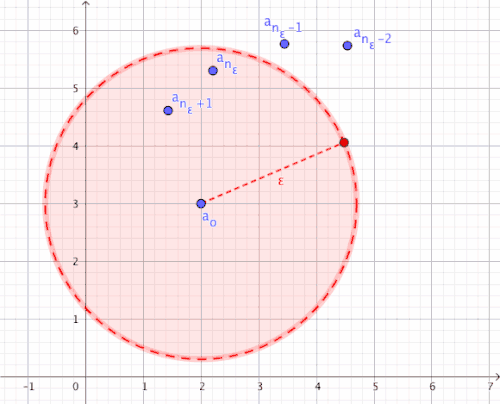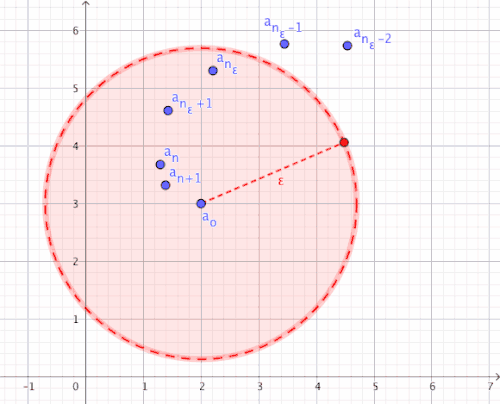
For all ${\textstyle \varepsilon >0}$ there is an index bound ${\textstyle n_{\varepsilon }}$ from which all components ${\textstyle a_{n}}$ of the sequence are an element of ${\displaystyle \varepsilon }$ environment of ${\displaystyle a_{o}}$ (i.e. ${\textstyle a_{n}\in \,\,]a_{o}-\varepsilon ,a_{o}+\varepsilon [}$

Semantics

The meaning of the definition can be promised as follows:

$${\displaystyle \lim _{n\to \infty }a_{n}=a_{0}:\Leftrightarrow \forall \varepsilon >0\;\exists n_{\varepsilon }\in \mathbb {N} \;\forall n\geq n_{\varepsilon }:\;\left|a_{n}-a_{0}\right|<\varepsilon }$$.

For an arbitrarily small ${\displaystyle \varepsilon >0}$ and you can always find an index bound ${\textstyle n_{\varepsilon }\in \mathbb {N} }$ from distance to ${\displaystyle a_{o}}$ is smaller than ${\displaystyle \varepsilon }$ (i.e. ${\displaystyle |a_{m}-a_{o}|<\varepsilon }$

Convergence of series

If the underlying vector space has a topology (e.g. generated by a metric space or a norm then the convergence of a series can be expression in analogue way ${\textstyle \displaystyle \sum _{k=1}^{\infty }a_{k}}$ converges if the associated sequence of the partial sums ${\textstyle (s_{n})_{n\in \mathbb {N} }:=\displaystyle \left(\sum _{k=1}^{n}a_{k}\right)_{n\in \mathbb {N} }}$ converges as sequence in vector space.

Absolute convergence

A series ${\textstyle \sum _{k=1}^{\infty }a_{k}}$ is absolutely convergent when the series ${\textstyle \sum _{k=1}^{\infty }|a_{k}|}$converges, i.e. the sequence of the partial sums ${\textstyle (s_{n})_{n\in \mathbb {N} }:=\left(\sum _{k=1}^{n}|a_{k}|\right)_{n\in \mathbb {N} }}$ converges in ${\displaystyle \mathbb {C} }$.

Learning Tasks

• Prove that the complex series ${\textstyle \sum _{k=1}^{\infty }(-1)^{k}\cdot {\frac {1}{k}}\cdot i}$ converges in ${\displaystyle \mathbb {C} }$, but does not converge absolutely. Use a theorem and your knowledge from calculus.
• Check the following series ${\textstyle \sum _{k=1}^{\infty }(i)^{k}\cdot 2^{-k+2}}$ for convergence. Calculate the first components of the partial sum as plot those numbers in the Gaussian number in a coordinate system. Explain why the sequence of the partial sums have these geometric properties. Calculate the limit of the series if it exists.

Series as mathematical object

The term ${\displaystyle \sum _{k=1}^{\infty }a_{k}}$ of a series does not denote sequence of partial sums ${\textstyle (s_{n})_{n\in \mathbb {N} }}$. In the case of a convergence the expression ${\displaystyle \sum _{k=1}^{\infty }a_{k}}$ defines a complex number as a limit of the sequence of partial sums:

${\displaystyle \sum _{k=1}^{\infty }a_{k}=\lim _{n\to \infty }s_{n}}$

with ${\displaystyle s_{n}:=\sum _{k=1}^{n}|a_{k}|.}$

Notation

For the limit value ${\textstyle s_{0}\in \mathbb {C} }$ of a series ${\textstyle \sum _{n=1}^{\infty }a_{n}}$ with ${\textstyle (a_{n})_{n\in \mathbb {N} }\in \mathbb {C} ^{\mathbb {N} }}$, you write:

${\textstyle \sum _{n=1}^{\infty }a_{n}=s_{0}}$

Convergence of Series

Be ${\textstyle (a_{n})_{n\in \mathbb {N} }\in \mathbb {C} ^{\mathbb {N} }}$ a complex number sequence and ${\textstyle s_{0}\in \mathbb {C} }$. The convergence of the series refers to the convergence of the partial sums ${\textstyle s_{n}=\sum _{k=1}^{n}a_{k}}$ against ${\textstyle s_{0}}$, i.e.:

$${\displaystyle \sum _{n=1}^{\infty }a_{n}=s_{0}:\Leftrightarrow \forall \varepsilon >0\;\exists n_{\varepsilon }\in \mathbb {N} \;\forall n\geq n_{\varepsilon }:\;\left|s_{n}-s_{0}\right|<\varepsilon .}$$

This applies ${\textstyle \left|s_{n}-s_{0}\right|=\left|\sum _{k=1}^{n}a_{k}-s_{0}\right|<\varepsilon }$.

Topological vector space

The topological vector space ${\textstyle V}$

• an additive operation to calculate vectors for the partial sums ${\textstyle s_{n}:=\sum _{k=1}^{n}a_{n}}$
• a topology to be able to investigate the convergence of the sequence of partial sums ${\textstyle (s_{n})_{n\in \mathbb {N} }}$.

Task - series convergence in a topological vector space

Let ${\textstyle a_{n}:={\begin{pmatrix}2^{-n}\\3^{-n}\\4^{-n}\end{pmatrix}}\in \mathbb {R} ^{3}}$. Calculate the limit of the series ${\textstyle g:=\sum _{k=0}^{\infty }a_{n}\in \mathbb {R} ^{3}}$ as an introductory example with the tools of the analysis! Explain the similarities and differences of the series convergence in topological vector spaces and the special case ${\textstyle \mathbb {C} }$. Transfer the definition convergence sequences or series to topological vector spaces ${\textstyle (V,\|\cdot \|)}$. What are the similarities and differences?

Topological algebra - potency series

Let ${\textstyle A}$ be a given topological algebra, then denote the algebra of power series by ${\textstyle {\overline {A[t]}}}$

• with a topology on the algebra ${\textstyle {\overline {A[t]}}}$ is the topological closure on the algebra ${\textstyle A[t]}$ of polynomial with coefficients
• an topology is generated by summation of the weighted vector lengths of the coefficients,
• additive and multiplicative operation can also be defined similar to the agebra polynomials ${\textstyle A[t]}$ and the algebra of power series ${\textstyle {\overline {A[t]}}}$.

Example - Polynomial Algebra and Convex Combinations

In the vector space ${\textstyle n\in \mathbb {N} }$ in the vector space ${\textstyle \mathbb {R} ^{3}}$, these polynomials of the order 3 represent With CAS4Wiki, the track of the three-dimensional convex combination of the order 3 can be plotted. CAS4Wiki Commands

Wiki2Reveal

The Wiki2Reveal slides were created for the Complex Analysis' and the Link for the Wiki2Reveal Slides was created with the link generator.

• This page is designed as a PanDocElectron-SLIDE document type.
• Source: Wikiversity https://en.wikiversity.org/wiki/Complex%20Analysis/Sequences%20and%20series
• see Wiki2Reveal for the functionality of Wiki2Reveal.

Translation and Version Control

This page was translated based on the following Wikiversity source page and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:

• Kurs:Funktionentheorie/Folgen und Reihen https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Folgen%20und%20Reihen
• Date: 11/2/2024
• Wikipedia2Wikiversity-Converter: https://niebert.github.com/Wikipedia2Wikiversity