Complex square root

Introduction

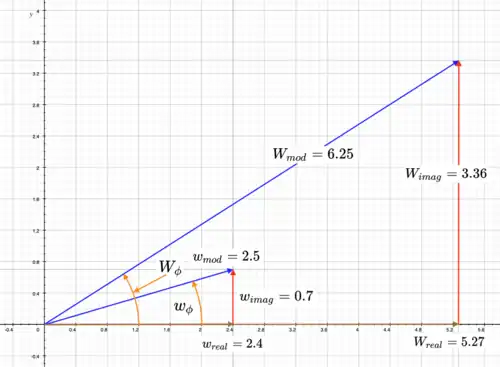Complex number W = complex number w².
Origin at point

(0,0)

.

w_{real},W_{real}

parallel to

X

axis.

w_{imag},W_{imag}

parallel to

Y

axis.

w_{real}=2.4;\ w_{imag}=0.7;\ w_{mod}={\sqrt {2.4^{2}+0.7^{2}}}=2.5.

W_{real}=5.27;\ W_{imag}=3.36;\

W_{mod}={\sqrt {5.27^{2}+3.36^{2}}}=6.25.

W_{mod}=w_{mod}^{2}=2.5^{2}=6.25.

W_{\phi }=2w_{\phi }.

By cosine double angle formula:

\cos W_{\phi }=\cos(2w_{\phi })=2\cos ^{2}w_{\phi }-1=2\cdot {\frac {2.4}{2.5}}\cdot {\frac {2.4}{2.5}}-1=0.8432={\frac {5.27}{6.25}}

Let complex numbers $W=a+b\cdot i$ and $w=p+q\cdot i.$

Let $W=w^{2}.$

When given $a,b,$ aim of this page is to calculate $p,q.$

In the diagram complex number $w=p+qi=w_{real}+i\cdot w_{imag}=w_{mod}(\cos w_{\phi }+i\cdot \sin w_{\phi }),$ where

$w_{real},w_{imag}$ are the real and imaginary components of $w,$ the rectangular components.

$w_{mod},w_{\phi }$ are the modulus and phase of $w,$ the polar components.

Similarly, $W_{real},W_{imag},W_{mod},W_{\phi }$ are the corresponding components of $W.$

$W_{real},W_{imag}$ are given. $W_{real},W_{imag}=a,b.$

$W=w^{2}=(w_{mod}(\cos w_{\phi }+i\cdot \sin w_{\phi }))^{2}$

$=w_{mod}^{2}(\cos(2w_{\phi })+i\cdot \sin(2w_{\phi }))$

$=W_{mod}(\cos(W_{\phi })+i\cdot \sin(W_{\phi }))$

$=W$

There are 3 significant calculations:

$W_{mod}={\sqrt[{2}]{a^{2}+b^{2}}}$

$w_{mod}={\sqrt[{2}]{W_{mod}}}$ and

$\cos w_{\phi }=\cos {\frac {W_{\phi }}{2}}.$

It is not necessary to calculate actual values of $w_{\phi },W_{\phi }.$

As with real math, there are 2 complex square roots, $(p+qi),\ (-p-qi).$

Implementation

In the python programming language a complex square root is available for floating point numbers with a precision of 15.

# python code:
>>> (5.27 + 3.36*1j) ** 0.5
(2.4+0.7000000000000001j)
>>> 
>>> (-18j) ** .5
(3-2.9999999999999996j)
>>>

Function cmath.sqrt() provides clean output:

# python code:
>>> import cmath
>>> cmath.sqrt (5.27 + 3.36*1j)
(2.4+0.7j)
>>> cmath.sqrt (-18j)
(3-3j)
>>>

If it is desired to calculate complex square root with precision greater than that available for python's floating point math, the following code using python's decimal module will do the job. The following code also shows how complex square root is calculated.

# python code:
import decimal

dD = decimal.Decimal
dgt = decimal.getcontext()
Precision = dgt.prec = 100   # Adjust as necessary.

def ComplexSquareRoot (v1, v2 = None) :
    '''
p,q = ComplexSquareRoot (a,b) or
p,q = ComplexSquareRoot ((a,b))
a,b are the real and imaginary parts of complex number W = (a+bi)
p,q are the real and imaginary parts of complex number w = (p+qi)
where W = w ** 2
This function preserves +/- 0 as calculated by python function cmath.sqrt().
'''
    thisName = 'ComplexSquareRoot (v1, v2 = None) :'
    if v2 == None : a,b = v1
    else : a,b = v1,v2

    dgt.prec += 3
    a,b = [ dD(str(v)) for v in (a,b) ]

    if b == 0 :
        if a == 0 : p,q = dD(0),b
        else :
            root = abs(a).sqrt()
            if a > 0: p,q = root, b
            else : p,q = dD(0), root.copy_sign(b)
    elif a == 0 :
        root = abs(b/2).sqrt()
        if b > 0 : p,q = root, root
        else : p,q = root, -root
    else :
        Wmod = (a**2 + b**2).sqrt()
        wmod = Wmod.sqrt()
        cosWφ = a/Wmod
#             2
# cos2A = 2cos A - 1
        coswφ = ((cosWφ + 1) / 2).sqrt()
        p = wmod * coswφ
        q = b /(2*p)

    dgt.prec -= 3
    return [ s.normalize() for s in (p,q) ]

Examples

# python code:

import cmath
sqrt = cmath.sqrt

for (a,b) in (
        (0.,0.), (0.,-0.), (-0.,0.), (-0.,-0.),
        (4,0.),  (4,-0.),  (-4,0.),  (-4,-0.),
        (0.,50), (0.,-50), (-0.,50), (-0.,-50),
        (-394200411798404114010884279663511687236816, 157994206778295991363266285626991662856270),
):
    result1 = ComplexSquareRoot (a,b)
    result2 = sqrt (complex(a,b))
    str1 = 'result1, result2' ; print (str1, eval(str1))

result1, result2 ([Decimal('0'), Decimal('0')], 0j)
result1, result2 ([Decimal('0'), Decimal('-0')], -0j)
result1, result2 ([Decimal('0'), Decimal('0')], 0j)
result1, result2 ([Decimal('0'), Decimal('-0')], -0j)

result1, result2 ([Decimal('2'), Decimal('0')], (2+0j))
result1, result2 ([Decimal('2'), Decimal('-0')], (2-0j))
result1, result2 ([Decimal('0'), Decimal('2')], 2j)
result1, result2 ([Decimal('0'), Decimal('-2')], -2j)

result1, result2 ([Decimal('5'), Decimal('5')], (5+5j))
result1, result2 ([Decimal('5'), Decimal('-5')], (5-5j))
result1, result2 ([Decimal('5'), Decimal('5')], (5+5j))
result1, result2 ([Decimal('5'), Decimal('-5')], (5-5j))

# Function ComplexSquareRoot() preserves precision of large numbers:
result1, result2 ([Decimal('123456789012345678935'), Decimal('639876543210987654321')], (1.2345678901234568e+20+6.398765432109876e+20j))

Method #2. Algebraic

Introduction

Let $W=a+b\cdot i$ and $w=p+q\cdot i.$

Let $W=w^{2}=(p+qi)^{2}=p^{2}-q^{2}+2pqi.$

Then:

$a=P-Q\ \dots \ (1)$ where $P,Q=p^{2},q^{2}.$

$b=2pq\ \dots \ (2)$

Square $(2):\ B=4PQ\ \dots \ (3)$ where $B=b^{2}$

$(1)*4P:\ 4Pa=4PP-4PQ\ \dots \ (4)$

From $(3),(4):\ 4Pa=4PP-B\ \dots \ (5)$

From $(5):\ 4PP-4aP-B=0\ \dots \ (6)$

From $(6):$ $P={\frac {4a\pm {\sqrt {16a^{2}-4(4)(-B)}}}{2(4)}}$ $={\frac {a\pm {\sqrt {a^{2}+b^{2}}}}{2}}$ $={\frac {a\pm W_{mod}}{2}}$

Implementation

# python code:

def ComplexSquareRoot_al (v1, v2=None) :
    '''
ComplexSquareRoot algebraic
p, q = ComplexSquareRoot_al (a, b) 
'''
    if v2 == None : a,b = v1
    else : a,b = v1,v2

    if 0 in (a,b) : return  ComplexSquareRoot (a,b) 

    dgt.prec += 3
    a,b = [ dD(str(v)) for v in (a,b) ]

    Wmod = (a**2 + b**2).sqrt()
    P1 = (a+Wmod)/2
    # P1 must be > 0.
    p = P1.sqrt() ; q = b / (2*p)
    
    dgt.prec -= 3
    return [ s.normalize() for s in (p,q) ]

Because function ComplexSquareRoot_al() contains only two calculations of .sqrt() and function ComplexSquareRoot() contains three, function ComplexSquareRoot_al() is significantly faster than function ComplexSquareRoot().

Links to related topics

The Python Standard Library: cmath.sqrt

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.