< Elasticity
Elasticity/Concentrated force on half plane
Concentrated force on a half-plane
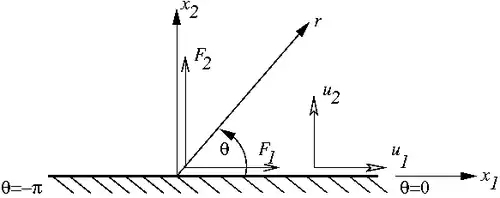 Concentrated force on a half plane |
From the Flamant Solution
and
If and, we obtain the special case of a concentrated force acting on a half-plane. Then,
or,
Therefore,
The stresses are
The stress is obviously the superposition of the stresses due to and , applied separately to the half-plane.
Problem 1 : Stresses and displacements due to F2
The tensile force produces the stress field
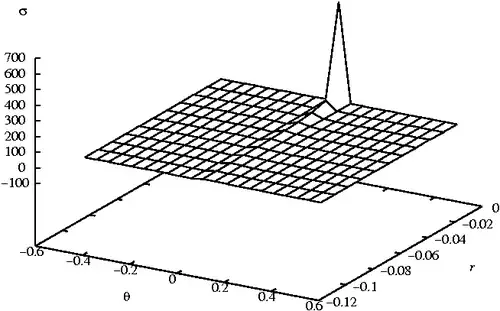 Stress due to concentrated force on a half plane |
The stress function is
Hence, the displacements from Michell's solution are
At , (, ),
At , (, ),
where
Since we expect the solution to be symmetric about , we superpose a rigid body displacement
The displacements are
where
and on .
Problem 2 : Stresses and displacements due to F1
The tensile force produces the stress field
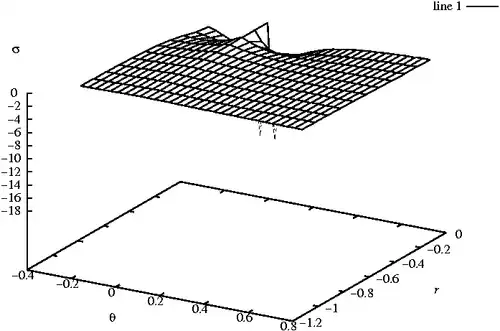 Stress due to concentrated force on a half plane |
The displacements are
Stresses and displacements due to F1 + F2
Superpose the two solutions. The stresses are
The displacements are
This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.