< Euclidean geometry 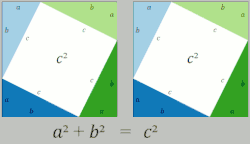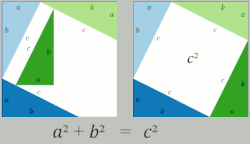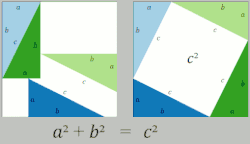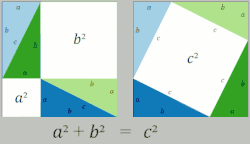
Euclidean geometry/Pythagorean theorem proofs
If you go back to Chapter 2 here, you'll see that in the introduction, we offered the Pythagorean Theorem as an example of a mathematical theorem that can be proven.
Well, here's a page that's going to show you just how true that is. Here are some hand-selected proofs (with additional commentary to facilitate learning) on proving the Pythagorean Theorem.
The Theorem Itself States...
For any right triangle with two legs a and b, and hypotenuse [the longest side] c, there is a relationship between the lengths of the three sides, such that
The length of side a times itself, plus the length of side b times itself, equals the length of side c, times itself.
Proof One:

As neither the size of the triangles nor the box they're contained in changes, the amount of empty space can't change either.
This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.