Holomorphic function/Criteria

Introduction

Holomorphy of a function $f\colon U\to \mathbb {C}$ at a point $z_{0}\in U$ is a neighborhood property of $z_{0}$ . There are numerous criteria in complex analysis that can be used to verify holomorphy. Let $U\subseteq \mathbb {C}$ be a domain as a subset of the complex plane and $z_{0}\in U$ a point in this subset.

Animation - Visualization of the Mapping

The animation shows the function $f(z)={\frac {1}{z}}$ . In the animation, $z$ is shown in blue, and the corresponding image point $f(z)$ is shown in red. The point $z$ and $f(z)$ are represented in $\mathbb {C} {\widetilde {=}}\mathbb {R} ^{2}$ . The $y$ -axis represents the imaginary part of the complex numbers $z$ and $f(z)$ . The blue point $z$ moves along the path $\gamma (t):=t\cdot (\cos(t)+i\cdot \sin(t))$

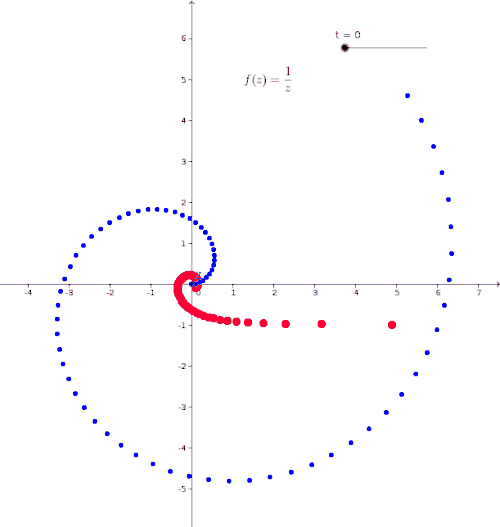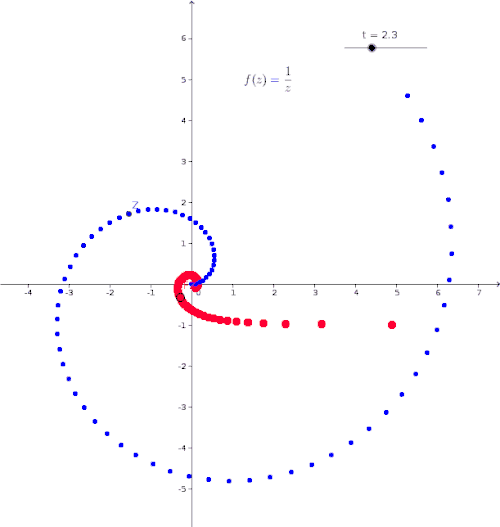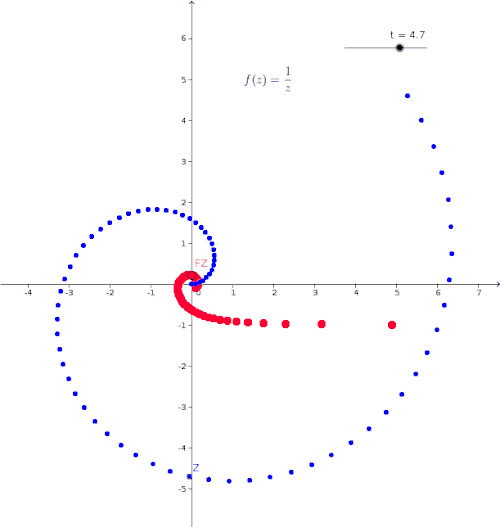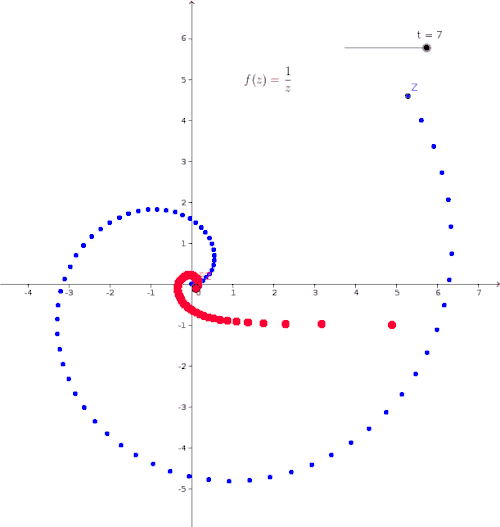
Animation

Complex Differentiability

A function $f\colon U\to \mathbb {C}$ is called complex differentiable at the point $z_{0}$ if the limit $\lim _{h\to 0}{\frac {f(z_{0}+h)-f(z_{0})}{h}}$ exists with $h\in \mathbb {C}$ . This is denoted as $f'(z_{0})$ .

Holomorphy

A function $f\colon U\to \mathbb {C}$ is called holomorphic at the point $z_{0}$ if there exists a neighborhood $U_{0}\subseteq U$ of $z_{0}$ such that $f$ is complex differentiable in $U_{0}$ . If $f$ is holomorphic on all of $U$ , it is simply called holomorphic. If additionally $U=\mathbb {C}$ , $f$ is called an entire function.

Holomorphy Criteria

Let $f:U\to \mathbb {C}$ be a function where $U\subseteq \mathbb {C}$ is a domain, then the following properties of the complex-valued function $f$ are equivalent:

(HK1) Once Complex Differentiable

The function $f$ is once complex differentiable on $U$ .

(HK2) Arbitrarily Often Complex Differentiable

The function $f$ is arbitrarily often complex differentiable on $U$ .

(HK3) Cauchy-Riemann Differential Equations

The real and imaginary parts satisfy the Cauchy-Riemann equations and are at least once continuously real-differentiable on $U$ .

(HK4) Locally Expansible in Power Series

The function can be locally expanded in a complex power series on $U$ .

(HK5) Path Integrals 0

The function $f$ is continuous, and the path integral of the function over any closed contractible path vanishes (i.e., the winding number of the path integral for all points outside of $U$ is 0).

(HK6) Cauchy Integral Formula

The function values inside a circular disk can be determined from the function values on the boundary using the Cauchy integral formula.

(HK7) Cauchy-Riemann Operator

$f$ is real differentiable, and ${\frac {\partial f}{\partial {\bar {z}}}}=0$ , where ${\frac {\partial }{\partial {\bar {z}}}}$ is the Cauchy-Riemann operator defined by ${\frac {\partial }{\partial {\bar {z}}}}:={\frac {1}{2}}\left({\frac {\partial }{\partial x}}+i{\frac {\partial }{\partial y}}\right)$ .

Exercises

Let $a,z_{0}\in \mathbb {C}$ be chosen arbitrarily, and assume that $a\neq z_{0}$ . Now, develop the function $f(z):={\frac {1}{z-a}}$ for $z\in \mathbb {C} \setminus {a}$ in a power series around $z_{0}\in \mathbb {C}$ and show that the following holds: $f(z)={\frac {1}{z-a}}=\sum _{n=0}^{\infty }-{\frac {1}{(a-z_{0})^{n+1}}}\cdot (z-z_{0})^{n}$

Calculate the radius of convergence of the power series! Explain why the radius of convergence depends on $a,z_{0}\in \mathbb {C}$ in this way and cannot be larger!

It is not true in real analysis that the existence of a once differentiable function implies that the function is infinitely differentiable. Consider the function $g(x):=x\cdot |x|$ defined on all of $\mathbb {R}$ .

Explain how the central theorem of Complex Analysis from criterion 1 leads to criterion 2!

Page Information

You can display this page as Wiki2Reveal slides

Wiki2Reveal

The Wiki2Reveal slides were created for the Holomorphic function' and the Link for the Wiki2Reveal Slides was created with the link generator.

This page is designed as a PanDocElectron-SLIDE document type.
Source: Wikiversity https://en.wikiversity.org/wiki/Holomorphic%20function/Criteria
see Wiki2Reveal for the functionality of Wiki2Reveal.

Translation and Version Control

This page was translated based on the following Wikiversity source page and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:

Source: Holomorphie/Kriterien
URL: https://de.wikiversity.org/wiki/Holomorphie/Kriterien
Date: 12/10/2024 9:56pm

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.