OpenStax University Physics/V2
Temperature and Heat
relates Celsius to Fahrenheit temperature scales. relates Kelvin to Celsius.▭ Linear thermal expansion: relates a small change in length to the total length , where is the coefficient of linear expansion.
▭ For expansion in two and three dimensions: and ,
respectively.
▭ Heat transfer is where is the specific heat capacity. In a calorimeter,
▭ Latent heat due to a phase change is for melting/freezing and for evaporation/condensation.
▭ Heat conduction (power):
where is heat conductivity and is thickness and is area.
▭ is the radiative
energy transfer rate where is emissivity and is the Stefan–Boltzmann constant.
The Kinetic Theory of Gases
Ideal gas law: Pressure×Volume where is the number of moles and is an absolute temperature.
▭ is the number of particles. Gas constant = 8.3 J K−1/mol
▭ Avegadro's number: = 6.02×1023. Boltzmann's constant: = 1.38×10−23J/K.
▭ Van der Waals equation
▭ RMS speed where the overline denotes mean, is a particle's mass and is the molar mass.
▭ Mean free path where is the mean-free-time
▭ Internal energy of an ideal monatomic gas , where average kinetic energy of a particle.
▭ defines the molar heat capacity at constant volume.
▭ for ideal gas with degrees of freedom
▭ Maxwell–Boltzmann speed distribution
▭ Average speed ▭ Peak velocity
The First Law of Thermodynamics
(Pressure, volume, temperature) remain constant in an (isobaric, isochoric, isothermal) process. Heat is not transferred in an adiabatic process.
▭ Equation of state
▭ Work done by a system
▭ Internal energy is a sum over all particles of kinetic and potential energies
▭ First law (Q is heat going in and W is work done by as shown in the figure)
▭ is the molar heat capacity at constant volume
▭ for an adiabatic process in an ideal gas, where the heat capacity ratio
The Second Law of Thermodynamics
work done in a heat engine cycle.
▭ Efficiency
▭ Coefficient of performance for a refrigerator , and heat pump
▭ Entropy change (reversible process at constant temperature)
▭ for any cyclic process is path independent.
▭ for any closed system. for any isothermal process.
Electric Charges and Fields
Coulomb's Law where the vacuum permittivity 8.85×10−12 F/m.
Elementary charge = e = 1.602×10−19C (electrons have charge q=−e and protons have charge q=+e.)

▭ By superposition, where
▭ Electric field where is the field at due to charges at
▭ The field above an infinite wire and above
an infinite plane
▭ An electric dipole in a uniform electric field experiences the torque
Gauss's Law
Flux for a uniform electric field
in general.
▭ Closed surface integral
▭ Gauss's Law . In simple cases:
▭ Electric field just outside the surface of a conductor
Electric Potential
Electric potential . Change in potential energy
▭ Electron (proton) mass = 9.11×10−31kg (1.67× 10−27kg). Electron volt: 1 eV = 1.602×10−19J
▭ Near an isolated point charge where =8.99×109 N·m/C2 is the Coulomb constant.
▭ Work done to assemble N particles
▭ Electric potential due to N charges.
. For continuous charge . For a dipole,
.
▭ Electric field as gradient of potential
▭ Del operatornote: Cartesian Cylindrical Spherical
Capacitance
defines capacitance. For a parallel plate capacitor, where A is area and d is gap length.
▭ and
for a spherical and cylindrical capacitor, respectively
▭ For capacitors in series (parallel)
▭
▭ Stored energy density
▭ A dielectric with will decrease the capacitor's electric field and stored energy , but increase the capacitance due to the induced electric field
▭ , is the perpendicular area, and is current density. is electric field, where is resistivity.
▭ Resistivity varies with temperature as . Similarily, where is resistance (Ω)
▭ Ohm's law ▭ Power
Direct-Current Circuits
Terminal voltage where is the internal resistance and is the electromotive force.
▭ Resistors in series and parallel: ▭
▭ Kirchoff's rules. Loop: Junction:
▭ ▭ where
is internal resistance of each voltage source.
▭ Charging an RC (resistor-capacitor) circuit: and
where is RC time, and .
▭ Discharging an RC circuit: and
Magnetic Forces and Fields

 Mass spectrometer in special case that both magnetic fields are equal
Mass spectrometer in special case that both magnetic fields are equal
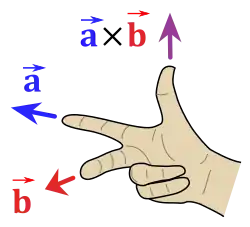
▭ is the force due to a magnetic field on a moving charge.
▭ For a current element oriented along .
▭ The SI unit for magnetic field is the Tesla: 1T=104 Gauss.
▭ Gyroradius Period
▭ Torque on current loop where is the dipole moment. Stored energy
▭ Drift velocity in crossed electric and magnetic fields
▭ Hall voltage = where the electric field is
▭ Charge-to-mass ratio where the and fields are crossed and when the magnetic field is
Sources of Magnetic Fields
.svg.png)
▭ Permeability of free space
T·m/A
▭ Force between parallel wires
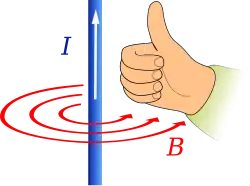
▭ Ampère's Law:
▭ Magnetic field due to long straight wire
▭ At center of loop
▭ Inside a long thin solenoid where is the ratio of the number of turns to the solenoid's length.
▭ Inside a toroid
▭ The magnetic field inside a solenoid filled with paramagnetic material is where is the permeability
Electromagnetic Induction
Magnetic flux
▭ Electromotive force (Faraday's law)
▭ Motional emf
▭ rotating coil
▭ Motional emf around circuit
Inductance
The SI unit for inductance is the Henry: 1H=1V·s/A ▭ Mutual inductance: where is the flux through 1 due to the current in 2 and is the emf in 1. Likewise, it can be shownSEE TALK that, .

▭ Self-inductance ▭ Stored energy
▭ is the current in an LR circuit where is the LR decay time.
▭ The capacitor's charge on an LC circuit
where is angular frequency
▭ LRC circuit where
Alternating-Current Circuits
AC voltage and current if
▭ RMS values and ▭ Impedance
▭ Resistor where
▭ Capacitor where
▭ Inductor where
▭ RLC series circuit where and
▭ Resonant angular frequency
▭ Quality factor
▭ Average power , where for a resistor.
▭ Transformer voltages and currents
Electromagnetic Waves
Displacement current where is the electric flux.
Maxwell's equations
See also http://ethw.org/w/index.php?title=Maxwell%27s_Equations&oldid=157445
▭ Plane EM wave equation where is the speed of light
▭ The ratio of peak electric to magnetic field is and the Poynting vector represents the energy flux
▭ Average intensity
▭ Radiation pressure (perfect absorber) and (perfect reflector).
