Tesseract and 16-cell faces

This list shows the $3^{4}=81$ k-faces of the tesseract and its dual 16-cell.

tesseract projection
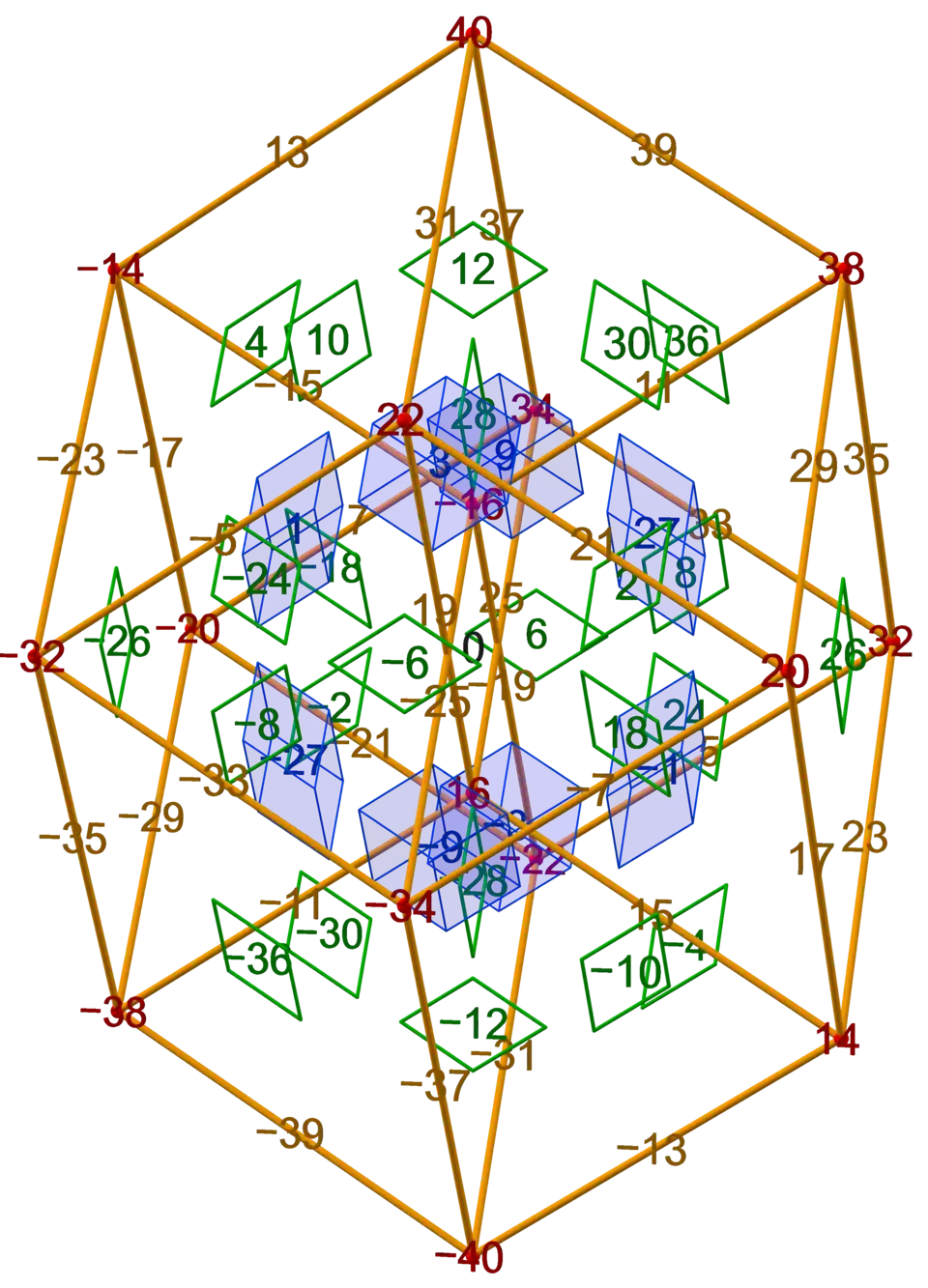Tesseract k-faces with labels from −40 to 40	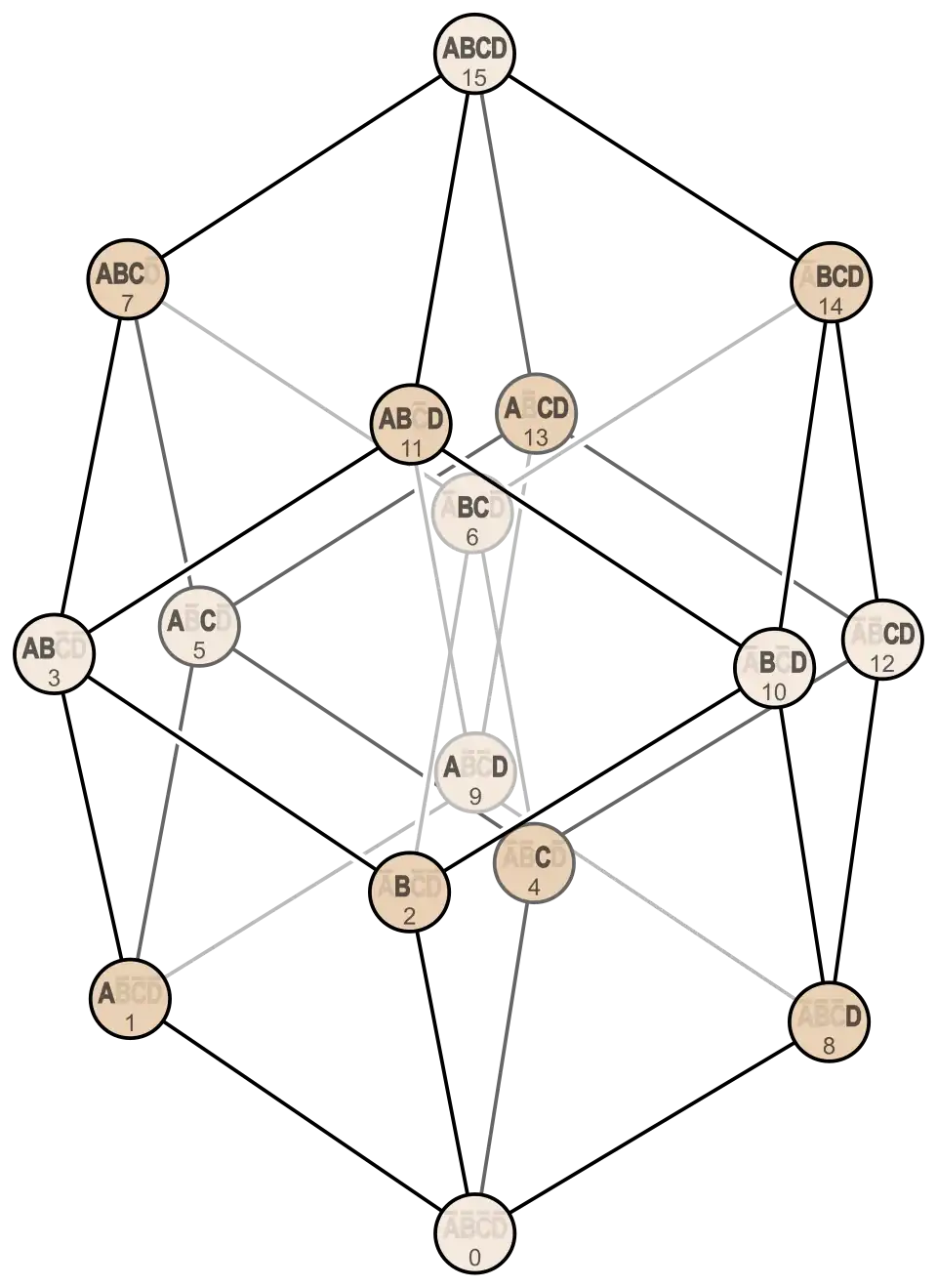Tesseract vertices with labels from 0 to 15
The convex hull of this projection is the Bilinski dodecahedron. A map from k-faces (−40 to 40) to lists of tesseract vertices (0 to 15) can be found here.

16-cell projection
8 vertices	24 edges (forming 6 rings)	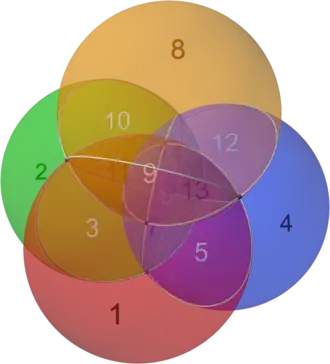32 triangular faces (forming 4 spheres)	graph corresponding to 15 of 16 cells

ternary weight	0	1	2	3	4
number of faces	0	8	24	32	16
tesseract faces	t 4 tesseract	t 3 cube	t 2 square	t 1 edge	t 0 vertex
16-cell faces	c 4 16-cell	c 0 vertex	c 1 edge	c 2 triangle	c 3 tetrahedron

The sign vectors (with entries 1, 0, −1) in the following table are the face centers of the tesseract. (Compare example for the cube.)
The indices on the left (between −40 and 40) are their interpretation as little-endian balanced ternary numbers.
The columns to their right are their sums, patterns of non-zero entries, and Hamming weights (numbers of non-zero entries).
The default order of the table is first by Hamming weights, then by patterns, and then by sums.

index	s	p	w	tesseract face type	tesseract vertices	16-cell face type
0	0	0 ....	0	t 4 tesseract	!!!! !!!! !!!! !!!!	c 4 16-cell
−1	−1	1 !...	1	t 3 cube	!.!. !.!. !.!. !.!.	c 0 vertex
1	1	1 !...	1	t 3 cube	.!.! .!.! .!.! .!.!	c 0 vertex
−3	−1	2 .!..	1	t 3 cube	!!.. !!.. !!.. !!..	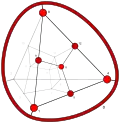c 0 vertex
3	1	2 .!..	1	t 3 cube	..!! ..!! ..!! ..!!	c 0 vertex
−9	−1	4 ..!.	1	t 3 cube	!!!! .... !!!! ....	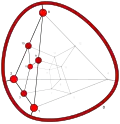c 0 vertex
9	1	4 ..!.	1	t 3 cube	.... !!!! .... !!!!	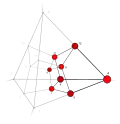c 0 vertex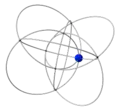
−27	−1	8 ...!	1	t 3 cube	!!!! !!!! .... ....	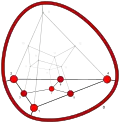c 0 vertex
27	1	8 ...!	1	t 3 cube	.... .... !!!! !!!!	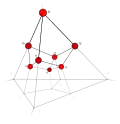c 0 vertex
−4	−2	3 !!..	2	t 2 square	!... !... !... !...	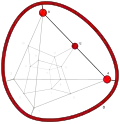c 1 edge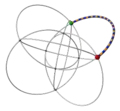
−2	0	3 !!..	2	t 2 square	.!.. .!.. .!.. .!..	c 1 edge
2	0	3 !!..	2	t 2 square	..!. ..!. ..!. ..!.	c 1 edge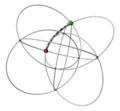
4	2	3 !!..	2	t 2 square	...! ...! ...! ...!	c 1 edge
−10	−2	5 !.!.	2	t 2 square	!.!. .... !.!. ....	c 1 edge
−8	0	5 !.!.	2	t 2 square	.!.! .... .!.! ....	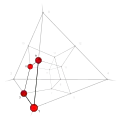c 1 edge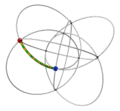
8	0	5 !.!.	2	t 2 square	.... !.!. .... !.!.	c 1 edge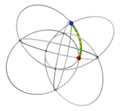
10	2	5 !.!.	2	t 2 square	.... .!.! .... .!.!	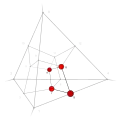c 1 edge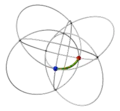
−12	−2	6 .!!.	2	t 2 square	!!.. .... !!.. ....	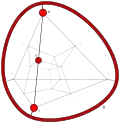c 1 edge
−6	0	6 .!!.	2	t 2 square	..!! .... ..!! ....	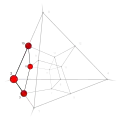c 1 edge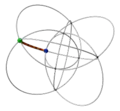
6	0	6 .!!.	2	t 2 square	.... !!.. .... !!..	c 1 edge
12	2	6 .!!.	2	t 2 square	.... ..!! .... ..!!	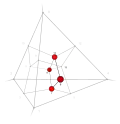c 1 edge
−28	−2	9 !..!	2	t 2 square	!.!. !.!. .... ....	c 1 edge
−26	0	9 !..!	2	t 2 square	.!.! .!.! .... ....	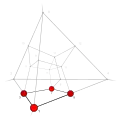c 1 edge
26	0	9 !..!	2	t 2 square	.... .... !.!. !.!.	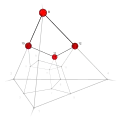c 1 edge
28	2	9 !..!	2	t 2 square	.... .... .!.! .!.!	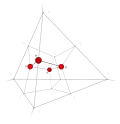c 1 edge
−30	−2	10 .!.!	2	t 2 square	!!.. !!.. .... ....	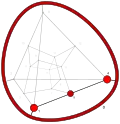c 1 edge
−24	0	10 .!.!	2	t 2 square	..!! ..!! .... ....	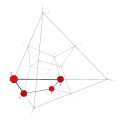c 1 edge
24	0	10 .!.!	2	t 2 square	.... .... !!.. !!..	c 1 edge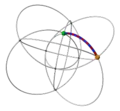
30	2	10 .!.!	2	t 2 square	.... .... ..!! ..!!	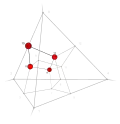c 1 edge
−36	−2	12 ..!!	2	t 2 square	!!!! .... .... ....	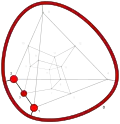c 1 edge
−18	0	12 ..!!	2	t 2 square	.... !!!! .... ....	c 1 edge
18	0	12 ..!!	2	t 2 square	.... .... !!!! ....	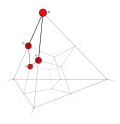c 1 edge
36	2	12 ..!!	2	t 2 square	.... .... .... !!!!	c 1 edge
−13	−3	7 !!!.	3	t 1 edge	0, 8	c 2 triangle
−11	−1	7 !!!.	3	t 1 edge	1, 9	c 2 triangle
−7	−1	7 !!!.	3	t 1 edge	2, 10	c 2 triangle
5	−1	7 !!!.	3	t 1 edge	4, 12	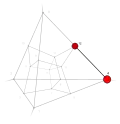c 2 triangle
−5	1	7 !!!.	3	t 1 edge	3, 11	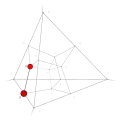c 2 triangle
7	1	7 !!!.	3	t 1 edge	5, 13	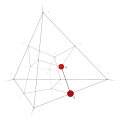c 2 triangle
11	1	7 !!!.	3	t 1 edge	6, 14	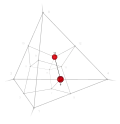c 2 triangle
13	3	7 !!!.	3	t 1 edge	7, 15	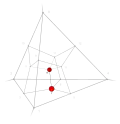c 2 triangle
−31	−3	11 !!.!	3	t 1 edge	0, 4	c 2 triangle
−29	−1	11 !!.!	3	t 1 edge	1, 5	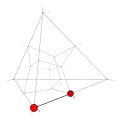c 2 triangle
−25	−1	11 !!.!	3	t 1 edge	2, 6	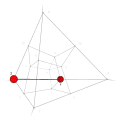c 2 triangle
23	−1	11 !!.!	3	t 1 edge	8, 12	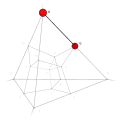c 2 triangle
−23	1	11 !!.!	3	t 1 edge	3, 7	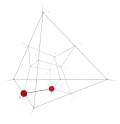c 2 triangle
25	1	11 !!.!	3	t 1 edge	9, 13	c 2 triangle
29	1	11 !!.!	3	t 1 edge	10, 14	c 2 triangle
31	3	11 !!.!	3	t 1 edge	11, 15	c 2 triangle
−37	−3	13 !.!!	3	t 1 edge	0, 2	c 2 triangle
−35	−1	13 !.!!	3	t 1 edge	1, 3	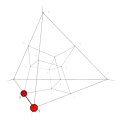c 2 triangle
−19	−1	13 !.!!	3	t 1 edge	4, 6	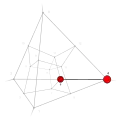c 2 triangle
17	−1	13 !.!!	3	t 1 edge	8, 10	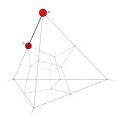c 2 triangle
−17	1	13 !.!!	3	t 1 edge	5, 7	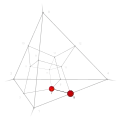c 2 triangle
19	1	13 !.!!	3	t 1 edge	9, 11	c 2 triangle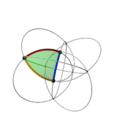
35	1	13 !.!!	3	t 1 edge	12, 14	c 2 triangle
37	3	13 !.!!	3	t 1 edge	13, 15	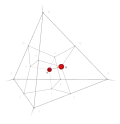c 2 triangle
−39	−3	14 .!!!	3	t 1 edge	0, 1	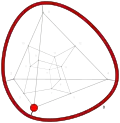c 2 triangle
−33	−1	14 .!!!	3	t 1 edge	2, 3	c 2 triangle
−21	−1	14 .!!!	3	t 1 edge	4, 5	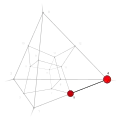c 2 triangle
15	−1	14 .!!!	3	t 1 edge	8, 9	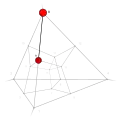c 2 triangle
−15	1	14 .!!!	3	t 1 edge	6, 7	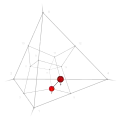c 2 triangle
21	1	14 .!!!	3	t 1 edge	10, 11	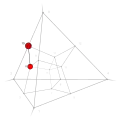c 2 triangle
33	1	14 .!!!	3	t 1 edge	12, 13	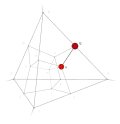c 2 triangle
39	3	14 .!!!	3	t 1 edge	14, 15	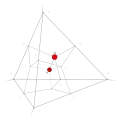c 2 triangle
−40	−4	15 !!!!	4	t 0 vertex	0	c 3 tetrahedron
−38	−2	15 !!!!	4	t 0 vertex	1	c 3 tetrahedron
−34	−2	15 !!!!	4	t 0 vertex	2	c 3 tetrahedron
−22	−2	15 !!!!	4	t 0 vertex	4	c 3 tetrahedron
14	−2	15 !!!!	4	t 0 vertex	8	c 3 tetrahedron
−32	0	15 !!!!	4	t 0 vertex	3	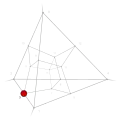c 3 tetrahedron
−20	0	15 !!!!	4	t 0 vertex	5	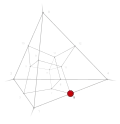c 3 tetrahedron
−16	0	15 !!!!	4	t 0 vertex	6	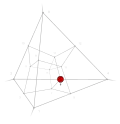c 3 tetrahedron
16	0	15 !!!!	4	t 0 vertex	9	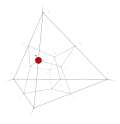c 3 tetrahedron
20	0	15 !!!!	4	t 0 vertex	10	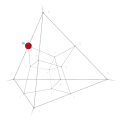c 3 tetrahedron
32	0	15 !!!!	4	t 0 vertex	12	c 3 tetrahedron
−14	2	15 !!!!	4	t 0 vertex	7	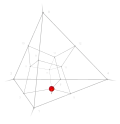c 3 tetrahedron
22	2	15 !!!!	4	t 0 vertex	11	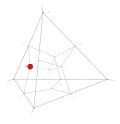c 3 tetrahedron
34	2	15 !!!!	4	t 0 vertex	13	c 3 tetrahedron
38	2	15 !!!!	4	t 0 vertex	14	c 3 tetrahedron
40	4	15 !!!!	4	t 0 vertex	15	c 3 tetrahedron

Python fragment

face_to_signs = {-40: '−−−−',  -39: '0−−−',  -38: '+−−−',  -37: '−0−−',  -36: '00−−',  -35: '+0−−',  -34: '−+−−',  -33: '0+−−',  -32: '++−−',  -31: '−−0−',  -30: '0−0−',  -29: '+−0−',  -28: '−00−',  -27: '000−',  -26: '+00−',  -25: '−+0−',  -24: '0+0−',  -23: '++0−',  -22: '−−+−',  -21: '0−+−',  -20: '+−+−',  -19: '−0+−',  -18: '00+−',  -17: '+0+−',  -16: '−++−',  -15: '0++−',  -14: '+++−',  -13: '−−−0',  -12: '0−−0',  -11: '+−−0',  -10: '−0−0',  -9: '00−0',  -8: '+0−0',  -7: '−+−0',  -6: '0+−0',  -5: '++−0',  -4: '−−00',  -3: '0−00',  -2: '+−00',  -1: '−000',  0: '0000',  1: '+000',  2: '−+00',  3: '0+00',  4: '++00',  5: '−−+0',  6: '0−+0',  7: '+−+0',  8: '−0+0',  9: '00+0',  10: '+0+0',  11: '−++0',  12: '0++0',  13: '+++0',  14: '−−−+',  15: '0−−+',  16: '+−−+',  17: '−0−+',  18: '00−+',  19: '+0−+',  20: '−+−+',  21: '0+−+',  22: '++−+',  23: '−−0+',  24: '0−0+',  25: '+−0+',  26: '−00+',  27: '000+',  28: '+00+',  29: '−+0+',  30: '0+0+',  31: '++0+',  32: '−−++',  33: '0−++',  34: '+−++',  35: '−0++',  36: '00++',  37: '+0++',  38: '−+++',  39: '0+++',  40: '++++'}

for face_int, face_signs in face_to_signs.items():
    indices = [i for i, x in enumerate(face_signs) if x != '0']
    weight = len(indices)
    tess_dim = 4 - weight
    cross_dim = [4, 0, 1, 2, 3][weight]
    tess_type = ['vertex', 'edge', 'square', 'cube', 'tesseract'][tess_dim]
    cross_type = ['vertex', 'edge', 'triangle', 'tetrahedron', '16-cell'][cross_dim]

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.