University of Florida/Egm3520/s13.team1.r6

R6.1 Solution

• We must first analyze the cross sectional area.

${\displaystyle A=30\cdot 24=720mm^{2}}$

• Next calculate the moment of inertia of the rectangular cross section.

${\displaystyle I={\frac {bd^{3}}{12}}={\frac {30\cdot 24^{3}}{12}}=34560mm^{4}}$

• Next calculate the centroid of the rectangle

${\displaystyle c={\frac {h}{2}}=12mm}$

• Next we show a free body diagram of the forces present on the bracket

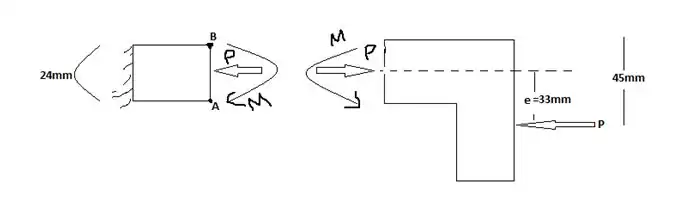
• Find the eccentricity

${\displaystyle e=45mm-{\frac {24}{2}}=33mm}$

• Calculate the bending couple using P = 8kN and e = 0.033m

${\displaystyle M={\color {blue}Pe}=8\cdot 0.033=264N*m}$

• Now we can calculate the stresses

${\displaystyle \sigma _{centric}={\color {blue}{\frac {-P}{A}}}={\frac {8\cdot 10^{3}}{7.2\cdot 10^{-4}}}=-11.11MPa}$

${\displaystyle \sigma _{bending}={\color {blue}{\frac {MC}{I}}}={\frac {264\cdot 0.012}{34560\cdot 10^{\left(-3\right)^{4}}}}=90.67MPa}$

• Stress induced at point A:

${\displaystyle \sigma _{A}=\sigma _{centric}-\sigma _{bending}=-11.11MPa-91.67MPa={\color {red}-102.78MPa}}$

• Stress induced at point B:

${\displaystyle \sigma _{B}=\sigma _{centric}+\sigma _{bending}=-11.11MPa+91.67MPa={\color {red}80.56MPa}}$

R6.3 Solution

GIVEN

Term	Desig	Value
Outer Diameter	${\displaystyle d_{o}}$	${\displaystyle 0.75in}$
Thickness	${\displaystyle t}$	${\displaystyle 0.08in}$
Inner Diameter	${\displaystyle d_{i}}$	${\displaystyle d_{i}=d_{o}-t=0.75-0.08(2)=0.59in}$
Area	${\displaystyle A}$	${\displaystyle {\frac {\pi }{4}}\left(d_{o}^{2}-d_{i}^{2}\right)={\frac {\pi }{4}}\left(0.75^{2}-0.59^{2}\right)\approx 0.168in^{2}}$
Stress	${\displaystyle \sigma }$	${\displaystyle \sigma ={\frac {P}{A}}}$

• The internal forces in the cross section are equivalent to a centric force P and a bending curve M. (*) Ex:4.07 on pg 272

• EQ 4.49 on page 270(*) states:

${\displaystyle {\color {blue}F=P\,\,\,\,\,\,\,\,\,\,M=Pd}}$

(Where F = Force at centroid, P = Line of action load, M = Moment, and d = offset distance.)

• EQ 4.5 on page 271(*) states:

${\displaystyle {\color {blue}\sigma _{x}={\frac {P}{A}}-{\frac {M\gamma }{I}}}}$

${\displaystyle \gamma ={\frac {d_{o}}{2}}=0.375in}$ (Distance from centroid)

• The Moment of Inertia of a Hollowed Cylindrical Cross-Section:

${\displaystyle {\color {blue}I={\frac {\pi }{64}}\left(d_{o}^{4}-d_{i}^{4}\right)}={\frac {\pi }{64}}\left(0.75^{4}-0.59^{4}\right)=0.00958in^{4}}$

• To ensure the the max stress does not exceed 4 times the stress in the tube and making an assumption that P = 1, we can derive the following solution:

${\displaystyle \sigma _{all}=4\sigma =4{\frac {P}{A}}}$

${\displaystyle \sigma _{all}={\frac {P}{A}}-{\frac {M\gamma }{I}}={\frac {P}{A}}-{\frac {Pd\gamma }{I}}}$

${\displaystyle \implies 4{\frac {P}{A}}={\frac {P}{A}}+{\frac {Pd\gamma }{I}}\implies {\frac {4}{A}}={\frac {1}{A}}+{\frac {d\gamma }{I}}\implies {\frac {3}{A}}={\frac {d\gamma }{I}}}$

${\displaystyle \implies {\frac {3}{0.168}}={\frac {d(0.375)}{0.00958}}\implies d={\color {red}+0.456in}}$

R6.4 Solution

• Max allowable stresses on the hanger:

${\displaystyle \sigma _{allow}=+5ksi}$ ${\displaystyle F_{max\downarrow }=?}$

${\displaystyle \sigma _{allow}=-12ksi}$ ${\displaystyle F_{max\uparrow }=?}$

• Find centroid:

• Take ${\displaystyle {\overline {y}}}$ as a distance measured from left end of shape.

${\displaystyle {\overline {Y}}={\frac {\sum {\overline {y}}A}{\sum A}}}$

${\displaystyle A_{1}=(3in)(1in)=3in^{2}}$

${\displaystyle A_{2}=(3in)(.75in)=2.25in^{2}}$

• Due to same parameters,

${\displaystyle A_{3}=A_{2}=2.25in^{2}}$

${\displaystyle {\overline {y_{1}}}={\frac {1}{2}}in=.5in}$

${\displaystyle {\overline {y_{2}}}=1in+{\frac {3}{2}}in=2.5in}$

• Due to same parameters,

${\displaystyle {\overline {y_{3}}}={\overline {y_{2}}}=2.5in}$

${\displaystyle \therefore {\overline {Y}}={\frac {(.5in)(3in)+(2.5in)(2.25in)+(2.5in)(2.25in)}{7.5in}}=1.7in}$

• Must incorporate the parallel axis theorem to find moment of inertia: ${\displaystyle {\color {blue}I={\frac {bh^{3}}{12}}+Ad^{2}}}$

b = base, h = height, A = area, and d = perpendicular distance between centroidal axis and parallel axis

${\displaystyle {\color {blue}I_{1}={\frac {b_{1}h_{1}^{3}}{12}}+A_{1}d_{1}^{2}}\,\,where\,\,{\color {blue}d_{1}=({\overline {y_{1}}}-{\overline {Y}})}\implies I_{1}={\frac {(3in)(1in)^{3}}{12}}+(3in^{2})(.5in-1.7in)^{2}=4.57in^{4}}$

${\displaystyle {\color {blue}I_{2}={\frac {b_{2}h_{2}^{3}}{12}}+A_{2}d_{2}^{2}}\,\,where\,\,{\color {blue}d_{2}=({\overline {y_{2}}}-{\overline {Y}})}\implies I_{1}={\frac {(.75in)(3in)^{3}}{12}}+(2.25in^{2})(2.5in-1.7in)^{2}=3.1275in^{4}}$

• Due to same parameters,

${\displaystyle I_{3}=I_{2}=3.1275in^{4}}$

${\displaystyle \therefore }$ Total moment of inertia is:${\displaystyle {\color {blue}I_{Tot}=I_{1}+I_{2}+I_{3}}=4.57in^{4}+3.1275in^{4}+3.1275in^{4}\implies 10.825in^{4}}$

• The normal stress at point A is due to bending:

${\displaystyle {\color {blue}\sigma _{bending}=-{\frac {My}{I}}}}$

• "The internal forces in the cross section are equivalent to a centric force P and a bending couple M " (Example Problem 4.07 page 272(*)):

${\displaystyle {\color {blue}M=Pd}\,\,\,\,\,{\color {blue}P=F_{max}=maximumforce}\,\,\,\,\,d=}$distance of the force from the centroid of the cross section. (EQ 4.49 page 270 (*))

Normal stress due to centric load: ${\displaystyle {\color {blue}\sigma _{centric}={\frac {P}{A}}}}$

• Combine:

${\displaystyle {\color {blue}\sigma =\sigma _{centric}+\sigma _{bending}={\frac {P}{A}}-{\frac {My}{I}}}}$ (EQ4.50, p.221(*))

${\displaystyle \uparrow =}$Total normal stress acting at point A.

• Largest downward force:

• Assuming conventions:${\displaystyle \sigma _{max}=+5ksi,A=7.5in^{2},I=10.825in^{4},y=-1.7in,d}$ = distance of acting force from the centroid ${\displaystyle =1.5+1.7=3.2in}$

${\displaystyle {\color {blue}\sigma _{max}={\frac {P_{max}}{A}}-{\frac {My}{I}}}={\frac {P_{max}}{A}}-{\frac {P_{max}dy}{I}}=P_{max}({\frac {1}{A}}-{\frac {dy}{I}})}$

${\displaystyle \implies P_{max\downarrow }={\frac {\sigma _{max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}={\frac {5ksi}{({\frac {1}{7.5in^{2}}}-{\frac {(3.2in)(-1.7in)}{10.825in^{4}}})}}=7.86kips}$

• Largest upward force:

${\displaystyle \sigma _{all}=-12ksi,\,A=7.5in^{2},\,I=10.825in^{4},\,y=4-1.7=2.3in,\,d=1.5+1.7=3.2in}$

${\displaystyle P_{max\uparrow }={\frac {\sigma _{max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}=21.955kips}$

• The limiting factor is at 7.86 kips force upward.

• Apply negative sign throughout equation:

${\displaystyle {\color {blue}\sigma _{max}={\frac {-P_{max}}{A}}-{\frac {-my}{I}}\implies P_{max}={\frac {-\sigma _{all/max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}}}$

• The Downward force becomes:

${\displaystyle \sigma _{all}=+5ksi,\,A=7.5in^{2},\,I=10.825in^{4},\,y=2.3in,\,d=3.2in}$

${\displaystyle \implies P_{max\downarrow }=9.15kips}$

• The Upward Force becomes:

${\displaystyle \sigma _{max}=-12ksi,\,A=7.5in^{2},\,I=10.825in^{4},\,y=2.3in,\,d=3.2in}$

${\displaystyle \implies P_{max\uparrow }=18.87kips}$

${\displaystyle \therefore }$ Limit is at ${\displaystyle {\color {red}9.15kips}}$

R6.5 Solution

3D Representation of Figure 4.115

• Max allowable stresses on the hanger:

${\displaystyle \sigma _{allow}=+5ksi}$ ${\displaystyle F_{max\downarrow }=?}$

${\displaystyle \sigma _{allow}=-12ksi}$ ${\displaystyle F_{max\uparrow }=?}$

• Find centroid:

• Take ${\displaystyle {\overline {y}}}$ as a distance measured from left end of shape.

${\displaystyle {\overline {Y}}={\frac {\sum {\overline {y}}A}{\sum A}}}$

${\displaystyle A_{1}=(3in)(1in)=3in^{2}}$

${\displaystyle A_{2}=(3in)(.75in)=2.25in^{2}}$

• Due to same parameters,

${\displaystyle A_{3}=A_{2}=2.25in^{2}}$

${\displaystyle {\overline {y_{1}}}={\frac {1}{2}}in=.5in}$

${\displaystyle {\overline {y_{2}}}=1in+{\frac {3}{2}}in=2.5in}$

• Due to same parameters,

${\displaystyle {\overline {y_{3}}}={\overline {y_{2}}}=2.5in}$

${\displaystyle \therefore {\overline {Y}}={\frac {(.5in)(3in)+(2.5in)(2.25in)+(2.5in)(2.25in)}{7.5in}}=1.7in}$

• Must incorporate the parallel axis theorem to find moment of inertia: ${\displaystyle {\color {blue}I={\frac {bh^{3}}{12}}+Ad^{2}}}$

b = base, h = height, A = area, and d = perpendicular distance between centroidal axis and parallel axis

${\displaystyle {\color {blue}I_{1}={\frac {b_{1}h_{1}^{3}}{12}}+A_{1}d_{1}^{2}}\,\,where\,\,{\color {blue}d_{1}=({\overline {y_{1}}}-{\overline {Y}})}\implies I_{1}={\frac {(3in)(1in)^{3}}{12}}+(3in^{2})(.5in-1.7in)^{2}=4.57in^{4}}$

${\displaystyle {\color {blue}I_{2}={\frac {b_{2}h_{2}^{3}}{12}}+A_{2}d_{2}^{2}}\,\,where\,\,{\color {blue}d_{2}=({\overline {y_{2}}}-{\overline {Y}})}\implies I_{1}={\frac {(.75in)(3in)^{3}}{12}}+(2.25in^{2})(2.5in-1.7in)^{2}=3.1275in^{4}}$

• Due to same parameters,

${\displaystyle I_{3}=I_{2}=3.1275in^{4}}$

${\displaystyle \therefore }$ Total moment of inertia is:${\displaystyle {\color {blue}I_{Tot}=I_{1}+I_{2}+I_{3}}=4.57in^{4}+3.1275in^{4}+3.1275in^{4}\implies 10.825in^{4}}$

• The normal stress at point A is due to bending:

${\displaystyle {\color {blue}\sigma _{bending}=-{\frac {My}{I}}}}$

• "The internal forces in the cross section are equivalent to a centric force P and a bending couple M " (Example Problem 4.07 page 272(*)):

${\displaystyle {\color {blue}M=Pd}\,\,\,\,\,{\color {blue}P=F_{max}=maximumforce}\,\,\,\,\,d=}$distance of the force from the centroid of the cross section. (EQ 4.49 page 270 (*))

Normal stress due to centric load: ${\displaystyle {\color {blue}\sigma _{centric}={\frac {P}{A}}}}$

• Combine:

${\displaystyle {\color {blue}\sigma =\sigma _{centric}+\sigma _{bending}={\frac {P}{A}}-{\frac {My}{I}}}}$ (EQ4.50, p.221(*))

${\displaystyle \uparrow =}$Total normal stress acting at point A.

• Largest downward force:

• Assuming conventions:${\displaystyle \sigma _{max}=+5ksi,A=7.5in^{2},I=10.825in^{4},y=+2.3in,d}$ = distance of acting force from the centroid ${\displaystyle =3.2in}$

${\displaystyle {\color {blue}\sigma _{max}={\frac {P_{max}}{A}}-{\frac {My}{I}}}={\frac {P_{max}}{A}}-{\frac {P_{max}dy}{I}}=P_{max}({\frac {1}{A}}-{\frac {dy}{I}})}$

${\displaystyle \implies P_{max\downarrow }={\frac {\sigma _{max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}={\frac {5ksi}{({\frac {1}{7.5in^{2}}}-{\frac {(3.8in)(-2.3in)}{10.825in^{4}}})}}={\color {Red}6.15kips}}$

• Largest upward force:
• Apply negative sign throughout equation:

${\displaystyle {\color {blue}\sigma _{max}={\frac {-P_{max}}{A}}-{\frac {-my}{I}}\implies P_{max}={\frac {-\sigma _{all/max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}}}$

${\displaystyle \sigma _{all}=+5ksi,\,A=7.5in^{2},\,I=10.825in^{4},\,y=-1.7in,\,d=3.2in}$

${\displaystyle P_{max\uparrow }={\frac {\sigma _{max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}={\color {Red}13.54kips}}$

Egm3520.s13.Jeandona (discuss • contribs) 12:47, 10 April 2013 (UTC)