University of Florida/Egm4313/IEA-f13-team10/R1

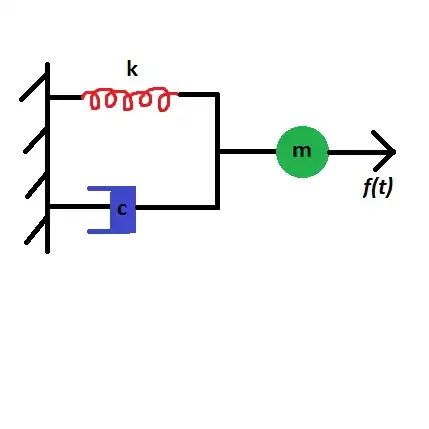
Kinematics

The spring and dashpot are in parallel, so the displacement of the spring is equal to the displacement of the dashpot.

(1) ${\displaystyle y=y_{k}=y_{c}}$

Kinetics

(2) ${\displaystyle my''+f_{I}=f(t)}$
(3) ${\displaystyle f_{I}=f_{k}+f_{c}}$

Constitutive Relations

(4) ${\displaystyle f_{k}=ky_{k}}$
(5) ${\displaystyle f_{c}=cy_{c}'}$

From (2), (3), (4) and (5), the equation of motion for the system is
${\displaystyle my''+cy_{c}'+ky_{k}=f(t)}$

From the first and second derivatives of (1),
${\displaystyle y'=y_{k}'=y_{c}'}$
${\displaystyle y''=y_{k}''=y_{c}''}$

So in terms of the displacement of the mass, the final equation of motion is,
${\displaystyle my''+cy'+ky=f(t)}$

Kinematics

The displacement of the spring equals the negative displacement of the dashpot (constitutive relation)

${\displaystyle y=y_{k}=-y_{c}}$

${\displaystyle y''=y''_{k}=-y''_{c}}$

Kinetics

Newton's second law ${\displaystyle {\vec {F}}=m{\vec {a}}}$

${\displaystyle r(t)=my''+r_{k}-r_{c}}$

${\displaystyle r_{k}=ky_{k}}$

${\displaystyle r_{c}=cy'_{c}}$

Substituting the relation above and kinematics section into the kinetics part, we get the equation of motion
${\displaystyle -my''_{c}-cy'_{c}+-ky_{c}=r(t)}$

Using the constitutive relations shown above we can write the equation of motion as
${\displaystyle my''+cy'+ky=r(t)}$

Step 1, Kinematics

${\displaystyle y=y_{k}+y_{c}}$, therefore ${\displaystyle y'=y'_{k}+y'_{c}}$ and ${\displaystyle y''=y''_{k}+y''_{c}}$

Step 2, FBD and Kinetics

${\displaystyle my''+f_{I}=f(t)}$

${\displaystyle f_{I}=f_{k}=f_{c}}$

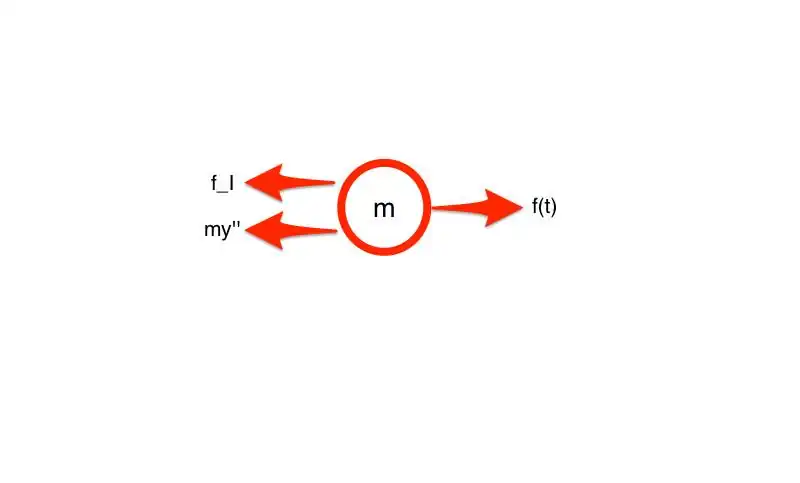
Step 3, Relations

${\displaystyle f_{k}=ky_{k}}$

${\displaystyle f_{c}=cy'_{c}}$

Step 4

${\displaystyle f_{k}=f_{c}}$, therefore ${\displaystyle ky_{k}=cy'_{c}}$, and ${\displaystyle y'_{c}={\frac {k}{c}}}$ and ${\displaystyle y''_{c}={\frac {k}{c}}y'_{k}}$

Step 5

Plugging the last equation from step 4 into the last equation from step 1, ${\displaystyle y''=y''_{k}+{\frac {k}{c}}y'_{k}}$

Step 6

Plugging the equation from step 5 into the first kinetic equation as y", ${\displaystyle m(y''_{k}+{\frac {k}{c}}y'_{k})+ky_{k}=f(t)}$

Derivation of (3) from (2)

(A) ${\displaystyle I={\frac {dQ}{dt}}=Cv'_{c}}$

(B) ${\displaystyle Q=Cv_{c}}$

Using equation A, we can show that ${\displaystyle LCv''_{c}=LI'}$ and ${\displaystyle RCv'_{c}=RI}$

Using equation B, we can show that ${\displaystyle v_{c}=Q/C}$

After these transformations, the new equation 2 is ${\displaystyle LI'+RI+{\frac {Q}{C}}=V}$

Taking the derivative of both sides of equation 2, we get ${\displaystyle LI''+RI'+{\frac {1}{C}}I=V'}$

Derivation of (4) from (2)

Using equation B, we can show that ${\displaystyle LCv''_{c}=LQ''}$ and ${\displaystyle RCv'_{c}=RQ'}$ and ${\displaystyle v_{c}={\frac {Q}{C}}}$

After these transformations, the new equation 2 is ${\displaystyle LQ''+RQ'+{\frac {Q}{C}}=V}$

Problem 3

${\displaystyle y''+6y'+8.96y=0}$

This is a linear, first order ODE with constant coefficients.

To find the general solution to this ODE set ${\displaystyle y=e^{rx}}$

so that ${\displaystyle y'=re^{rx}}$ and ${\displaystyle y''=r^{2}e^{rx}}$

Substituting in y to the ODE and factoring out ${\displaystyle e^{rx}}$ we get:

${\displaystyle r^{2}+6r+8.96=0}$

Using the quadratic formula to solve for r we get

${\displaystyle r={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$ where a = 1, b = 6, and c = 8.96

Solving to get r = -3.2 and r = -2.8

We get the general solution ${\displaystyle y(x)=C_{1}e^{-2.8x}+C_{2}e^{-3.2x}}$

Now with the initial values y(0) = 1 and y'(0) = .5

${\displaystyle y(0)=C_{1}+C_{2}=1}$

${\displaystyle y'(0)=-2.8C_{1}+-3.2C_{2}=.5}$

${\displaystyle C_{1}=9.25}$ , ${\displaystyle C_{2}=8.96}$

${\displaystyle y(x)=9.25e^{-2.8x}+8.96e^{-3.2x}}$

Problem 12

y′′+9 y′+20y=0

This is a linear, first order ODE with constant coefficients.

To find the general solution to this ODE set ${\displaystyle y=e^{rx}}$

so that ${\displaystyle y'=re^{rx}}$ and ${\displaystyle y''=r^{2}e^{rx}}$

Substituting in y to the ODE and factoring out ${\displaystyle e^{rx}}$ we get:

${\displaystyle r^{2}+9r+20=0}$

Using the quadratic formula to solve for r we get

${\displaystyle r={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$ where a = 1, b = 9, and c = 20

Solving to get r = -5 and r = -4

We get the general solution ${\displaystyle y(x)=C_{1}e^{-5x}+C_{2}e^{-4x}}$

Now with the initial values y(0) = 1 and y'(0) = .5

${\displaystyle y(0)=C_{1}+C_{2}=1}$

${\displaystyle y'(0)=-5C_{1}+-4C_{2}=.5}$

${\displaystyle C_{1}=-4.5}$ , ${\displaystyle C_{2}=5.5}$

${\displaystyle y(x)=9.25e^{-4.5x}+8.96e^{-5.5x}}$

Falling stone

(1) ${\displaystyle y''=g=const.}$

Equation (1) is the ODE that describes the acceleration of the stone as it falls from some height ${\displaystyle y=0}$ to the ground.
The highest order derivative of the dependent variable in an ODE determines the order of the ODE. In (1) the highest order derivative of the dependent variable y is second order. So (1) is a second-order ODE.

"A second-order ODE is called linear if it can be written ${\displaystyle y''+p(x)y'+q(x)y=r(x)}$" (Kreyszig 2011, p.46). Since (1) is in this form, with p(x) and q(x) = 0 and r(x) = g, then (1) is a linear ODE.

If the principle of superposition applies, then a solution ${\displaystyle {\bar {y}}(x)}$, which is comprised of the sum of the homogeneous solution ${\displaystyle y''_{h}+p(x)y'_{h}+q(x)y_{h}=0}$
and the particular solution ${\displaystyle y''_{p}+p(x)y'_{p}+q(x)y_{p}=r(x)}$, should satisfy the original ODE. So if superposition applies,
(2) ${\displaystyle y(x)={\bar {y}}(x)=y_{h}(x)+y_{p}(x)}$.
To determine whether superposition applies to (1), we consider
${\displaystyle y''_{h}+y''_{p}=0+g}$.
Now, using (2) and the linearity of the derivative,
${\displaystyle (y_{h}+y_{p})''=g}$
${\displaystyle {\bar {y}}''=g}$.
${\displaystyle {\bar {y}}}$ satisfies (1), so superposition can be applied.

Parachutist

(3) ${\displaystyle mv'=mg-bv^{2}}$

Since v' is the highest order derivative of the dependent variable v, (3) is a first-order ODE.

Because the dependent variable v is squared, (3) is a non-linear ODE.

${\displaystyle D(.)=m(.)'+b(.)^{2}}$
${\displaystyle D(w+y)=m(w+y)'+b(w+y)^{2}}$
D(w+y) does not equal f(w) + f(y) thus it is not linear.

Rearranging (3) we obtain ${\displaystyle mv'+bv^{2}=mg}$.
The homogeneous solution of the ODE is ${\displaystyle mv'_{h}+bv_{h}^{2}=0}$.
The particular solution of the ODE is ${\displaystyle mv'_{p}+bv_{p}^{2}=mg}$.
Using (2) and the linearity of the derivative we obtain ${\displaystyle m(v'_{h}+v'_{p})+b(v_{h}^{2}+v_{p}^{2})=0+mg}$
${\displaystyle m(v_{h}+v_{p})'=m{\bar {v}}'}$ but ${\displaystyle b(v_{h}^{2}+v_{p}^{2})\neq b(v_{h}+v_{p})^{2}}$
Therefore, ${\displaystyle {\bar {v}}}$ is not a solution to the ODE. So superposition cannot be applied.

Outflowing water

(4) ${\displaystyle h'=-k{\sqrt {h}}}$

(4) is a first-order ODE because of h' .

(4) is a non-linear ODE because of the square-rooted dependent variable h.

${\displaystyle D(.)=(.)'+k{\sqrt {.}}}$
${\displaystyle D(w+y)=(w+y)'+k{\sqrt {w+y}}}$
D(y+w) does not equal f(w)+f(y) so it is non-linear.

Rearranging (4) we obtain ${\displaystyle h'+k{\sqrt {h}}=0}$.
Summing the homogeneous and particular solutions we obtain ${\displaystyle (h'_{h}+h'_{p})+k({\sqrt {h_{h}}}+{\sqrt {h_{p}}})=0}$.
But ${\displaystyle {\sqrt {h_{h}}}+{\sqrt {h_{p}}}\neq {\sqrt {h_{h}+h_{p}}}}$.
So ${\displaystyle {\bar {h}}}$ is not a solution to (4), and superposition cannot be applied.

Vibrating mass on a spring

(5) ${\displaystyle my''+ky=0}$
(5) is a second-order linear ODE.

${\displaystyle m(y''_{h}+y''_{p})+k(y_{h}+y_{p})=0}$
${\displaystyle m{\bar {y}}''+k{\bar {y}}=0}$
${\displaystyle {\bar {y}}}$ satisfies (5), so superposition can be applied.

Beats of a vibrating system

(6) ${\displaystyle y''+\omega _{0}^{2}y=cos\omega t,\omega _{0}=\omega }$

(6) is a second-order linear ODE. Even with the ${\displaystyle \omega _{0}^{2}}$ and ${\displaystyle cos\omega t}$ terms, (6) is still linear because these are functions of the independent variable. We only look at the dependent variable when determining the linearity of an ODE.

${\displaystyle (y_{h}''+y_{p}'')+\omega _{0}^{2}(y_{h}+y_{p})=cos\omega t}$
${\displaystyle {\bar {y}}''+\omega _{0}^{2}{\bar {y}}=cos\omega t}$
${\displaystyle {\bar {y}}}$ satisfies (6), so superposition can be applied.

Current I in an RLC circuit

(7)${\displaystyle LI''+RI'+{\frac {1}{C}}I=E'}$

(7) is a second-order linear ODE.

${\displaystyle L(I_{h}''+I_{p}'')+R(I_{h}'+I_{p}')+{\frac {1}{C}}(I_{h}+I_{p})=E'}$
${\displaystyle L{\bar {I}}''+R{\bar {I}}'+{\frac {1}{C}}{\bar {I}}=E'}$
${\displaystyle {\bar {I}}}$ satisfies (7), so superposition can be applied.

Deformation of a beam

(8) ${\displaystyle EIy^{iv}=f(x)}$

(8) is a fourth-order linear ODE.

${\displaystyle EI(y_{h}^{iv}+y_{p}^{iv})=f(x)}$
${\displaystyle EI{\bar {y}}^{iv}=f(x)}$
${\displaystyle {\bar {y}}}$ satisfies (8), so superposition can be applied.

Pendulum

(9) ${\displaystyle L\theta ''+gsin\theta =0}$

(9) is a second-order non-linear ODE.

${\displaystyle L(\theta _{h}''+\theta _{p}'')+g(sin\theta _{h}+sin\theta _{p})=0}$
But ${\displaystyle sin\theta _{h}+sin\theta _{p}\neq sin(\theta _{h}+\theta _{p})}$
Therefore ${\displaystyle {\bar {\theta }}}$ is not a solution to (9), and superposition does not apply.