University of Florida/Egm4313/IEA-f13-team10/R5

Report 5

Problem 1: Taylor Series Expansion of the log Function

Problem Statement

$y''+6y'+9y=log(3+4x)$
$y(0)=1,y'(0)=.5$
Use the point
${\widehat {x}}=-1/2$
$\log x=\log _{e}x=\ln x$

Solution

$f(x)=\log(x)$
$f({\widehat {x}})=\log({\widehat {x}})$

$\sum _{k=0}^{\infty }{\frac {(f^{k})({\widehat {x}})}{k!}}(x-{\widehat {x}})^{k}$
$f^{1}(x)={\frac {1}{1+x}}=f^{1}({\widehat {x}})={\frac {1}{1+({\widehat {x}})}}$
Set
$w(x)=3+4x$
$w'(x)=4$

$f^{2}(x)={\frac {-1*w'*4}{w^{2}}}={\frac {-1}{w^{2}}}$

$f^{3}(x)={\frac {1*2*w*w'*4^{2}}{w^{4}}}={\frac {1*2}{w^{3}}}$

$f^{4}(x)={\frac {-1*2*3*w^{2}*w'*4^{3}}{w^{6}}}={\frac {-1*2*3}{w^{4}}}$

$f^{k}(x)={\frac {(-1)^{k-1}*(k-1)!*4^{k-1}}{w^{k}}}$

$\sum _{k=0}^{\infty }{\frac {(f^{k})({\widehat {x}})}{k!}}(x-{\widehat {x}})^{k}=\sum _{k=0}^{\infty }{\frac {(-1)^{k-1}(k-1)!}{k!(1+({\widehat {x}}))^{k}}}(x-{\widehat {x}})^{k}$

For $log(3+4x)$ the series expansion results in,
$\sum _{k=0}^{\infty }(-1)^{k+1}*({\frac {(2+4x)^{k}}{k}})$

Plots of taylor series expansion: Up to order 4

Up to order 7

Up to order 11

Up to order 16

The visually estimated domain of convergence is from .8 to .2.
Now use the transformation of variable
$x\longrightarrow t\ {\text{ such that }}\ 3+4x=1+t$
$x={\frac {t-2}{4}}$

If $log(1+t)$ has a domain of convergence from $[-1,+1]$ then $log(3+4x)$ converges from $[{\frac {-3}{4}},{\frac {-1}{4}}]$

Honor Pledge

On our honor, we solved this problem on our own, without aid from online solutions or solutions from previous semesters.

Problem 2: Plots of Truncated Series

Number 1

Plot at least 3 truncated series to show convergence

$\sum _{m=0}^{inf}{\frac {x^{2m+1}}{(2m+1)!}}$

m=0: $x$

m=1: $x+{\frac {x^{3}}{3*2*1}}$

m=2: $x+{\frac {x^{3}}{3*2*1}}+{\frac {x^{5}}{5*4*3*2*1}}$

Number 2

Plot at least 3 truncated series to show convergence

$\sum _{m=0}^{inf}({\frac {2}{3}})^{m}x^{2}m$

m=0: $x$

m=1: $x+{\frac {2}{3}}x^{2}$

m=2: $x+{\frac {2}{3}}x^{2}+{\frac {4}{9}}x^{4}$

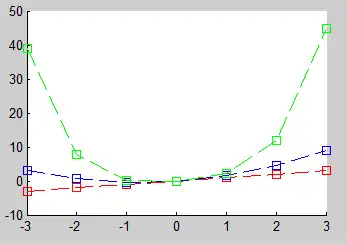
Number 3

Find the radius of convergence for the taylor series of sinx, x = 0

The Taylor series of sinx is:

$\sum _{m=0}^{inf}{\frac {(-1)^{m}(x)^{2m+1}}{(2m+1)!}}$

The radius of convergence can be found by:

$R_{c}=[lim\left|{\frac {d_{k+1}}{d_{k}}}\right|]^{-1}$

$R_{c}=[lim{\frac {(-1)^{m+1}}{(2m+3)!}}*{\frac {(2m+1)!}{(-1)^{m}}}]^{-1}$

$R_{c}=\infty$

Number 4

Find the radius of convergence for the taylor series of log(1+x), x = 0

The Taylor series of log(x+1) is:

$-\sum _{n=1}^{\infty }{\frac {(-1)^{n}(x)^{n}}{n}}$

The radius of convergence can be found by:

$R_{c}=[lim\left|{\frac {d_{k+1}}{d_{k}}}\right|]^{-1}$

$R_{c}=[lim{\frac {(-1)^{n+1}}{n+1}}*{\frac {n}{(-1)^{n}}}]^{-1}$
$R_{c}=1$

Number 5

Find the radius of convergence for the taylor series of log(1+x), x = 1

The Taylor series of log(x+1) is:

$-\sum _{n=1}^{\infty }{\frac {(-1)^{n}(x-1)^{n}}{n}}$

The radius of convergence can be found by:

$R_{c}=[lim\left|{\frac {d_{k+1}}{d_{k}}}\right|]^{-1}$

$R_{c}=[lim{\frac {(-1)^{n+1}}{n+1}}*{\frac {n}{(-1)^{n}}}]^{-1}$

$R_{c}=1$

Number 6

derive the expression for the radius of convergence of log(1+x) about any focus point

The taylor series of log(1+x) is:

$-\sum _{n=1}^{\infty }{\frac {(-1)^{n}(x-{\widehat {x}})^{n}}{n}}$

$R_{c}=[{\frac {(-1)^{n+1}({\widehat {x}})^{n+1}}{n+1}}*{\frac {n}{(-1)^{n}({\widehat {x}})^{n}}}]^{-1}$

Number 7

Find the Taylor series representation of log(3+4x)

$\sum _{k=0}^{\infty }{\frac {(f)^{k}({\widehat {x}})}{k!}}*(x-{\widehat {x}})^{k}$
Expanding out 4 terms results in,
[ $r(x)=0+{\frac {4*(x-{\widehat {x}})}{3+4{\widehat {x}}}}-{\frac {(4^{2})*((x-{\widehat {x}})^{2}}{((3+4{\widehat {x}})^{2})*(2!)}}+{\frac {2(4^{2})*((x-{\widehat {x}})^{3}}{((3+4{\widehat {x}})^{3})*(3!)}}$
The series representation is
$\sum _{k=0}^{\infty }(-1)^{k+1}*({\frac {(2+4x)^{k}}{k}})$

Number 8

Radius of convergence of log(3+4x) about the point ${\widehat {x}}=-.5$

${\widehat {x}}=-.5$
$\sum _{n=0}^{\infty }(-1)^{n+1}{\frac {4^{n}}{n}}(x+.5)^{n}$
$R_{c}=lim_{n\rightarrow \infty }[{(-1)^{n+2}}{\frac {4^{n+1}}{n+1}}(.25)^{n+1}*{\frac {n}{4^{n}(-1)^{n+1}(.25)^{n}}}]^{-1}$
Cancelling some terms out, you get
$R_{c}=lim_{n\rightarrow \infty }{\frac {-(n+1)}{n}}$
Using L'Hopitals Rule, you get
$R_{c}=lim_{n\rightarrow \infty }{\frac {1}{1}}=1$

Number 9

Radius of convergence of log(3+4x) about the point ${\widehat {x}}=-.25$

${\widehat {x}}=-.25$

$\sum _{n=0}^{\infty }(-1)^{n+1}{\frac {4^{n}}{n}}(x+.25)^{n}$
$R_{c}=lim_{n\rightarrow \infty }[{(-1)^{n+2}}{\frac {4^{n+1}}{n+1}}(.0625)^{n+1}*{\frac {n}{4^{n}(-1)^{n+1}(.0625)^{n}}}]^{-1}$
Cancelling some terms out, you get
$R_{c}=lim_{n\rightarrow \infty }{\frac {-4(n+1)}{n}}$
Using L'Hopitals Rule, you get
$R_{c}=lim_{n\rightarrow \infty }{\frac {4}{1}}=4$

Number 10

Radius of convergence of log(3+4x) about the point ${\widehat {x}}=1$

${\widehat {x}}=1$
$\sum _{n=0}^{\infty }(-1)^{n+1}{\frac {4^{n}}{n}}(x-1)^{n}$
$R_{c}=lim_{n\rightarrow \infty }[{(-1)^{n+2}}{\frac {4^{n+1}}{n+1}}(1)^{n+1}*{\frac {n}{4^{n}(-1)^{n+1}(1)^{n}}}]^{-1}$
Cancelling some terms out, you get
$R_{c}=lim_{n\rightarrow \infty }{\frac {-(n+1)}{4n}}$
Using L'Hopitals Rule, you get
$R_{c}=lim_{n\rightarrow \infty }{\frac {1}{4}}=1/4$

Number 11

Radius of convergence of log(3+4x) about any given point ${\widehat {x}}$

$\sum _{n=0}^{\infty }(-1)^{n+1}{\frac {4^{n}}{n}}(x-{\widehat {x}})^{n}$
$R_{c}=lim_{n\rightarrow \infty }[{(-1)^{n+2}}{\frac {4^{n+1}}{n+1}}({\widehat {x}}^{2})^{n+1}*{\frac {n}{4^{n}(-1)^{n+1}(({\widehat {x}}^{2})^{n})}}]^{-1}$

Honor Pledge

On our honor, we solved this problem on our own, without aid from online solutions or solutions from previous semesters.

Problem 3:

Problem Statement

Use the Determinant of the Matrix of Components and the Gramian to verify the linear independence of the two vectors $b_{1}$ and $b_{2}$ .

$\mathbf {b} _{1}=5\mathbf {e} _{1}-3\mathbf {e} _{2}$

$\mathbf {b} _{2}=-2\mathbf {e} _{1}+4\mathbf {e} _{2}$

Solution

Determinant of the Matrix of Components

The Matrix of components of the vectors $b_{1}$ and $b_{2}$ is

${\begin{vmatrix}5&-3\\-2&4\end{vmatrix}}=(5)(4)-(-3)(-2)=20-6=14\neq 0$

So the vectors $b_{1}$ and $b_{2}$ are linearly independent.

Gramian

For vectors, the Gramian is defined as:

$\ {\boldsymbol {\Gamma }}(b_{1},b_{2})={\begin{bmatrix}\langle b_{1},b_{1}\rangle &\langle b_{1},b_{2}\rangle \\\langle b_{2},b_{1}\rangle &\langle b_{2},b_{2}\rangle \end{bmatrix}}$

where:

$\ \langle b_{i},b_{j}\rangle =b_{i}\cdot b_{j}$

For the given vectors, the dot products are:

$\ \langle b_{1},b_{1}\rangle =(5e_{1}-3e_{2})\cdot (5e_{1}-3e_{2})=(5)(5)+(-3)(-3)=25+9=34$

$\ \langle b_{1},b_{2}\rangle =(5e_{1}-3e_{2})\cdot (-2e_{1}+4e_{2})=(5)(-2)+(-3)(4)=-10-12=-22$

$\ \langle b_{2},b_{1}\rangle =(-2e_{1}+4e_{2})\cdot (5e_{1}-3e_{2})=(-2)(5)+(4)(-3)=-10-12=-22$

$\ \langle b_{2},b_{2}\rangle =(-2e_{1}+4e_{2})\cdot (-2e_{1}+4e_{2})=(-2)(-2)+(4)(4)=4+16=20$

So the Gramian matrix becomes: $\ {\boldsymbol {\Gamma }}(b_{1},b_{2})={\begin{bmatrix}34&-22\\-22&20\end{bmatrix}}$

Finding the determinant of the Gramian matrix gives the Gramian:

$\ \Gamma =(34)(20)-(-22)(-22)=680-484=156\neq 0$

So the vectors $b_{1}$ and $b_{2}$ are linearly independent.

Honor Pledge

On our honor, we solved this problem on our own, without aid from online solutions or solutions from previous semesters.

Problem 4: Wronskian and Gramian

Problem Statement

Use both the Wronskian and the Gramain to find whether the following functions are linearly independent. Consider the domain of these functions to be [-1, +1] for the construction of the Gramian matrix.

$f(x)=x,g(x)=x^{5}$

$f(x)=cos2x,g(x)=sin4x$

Solution

Wronskian:

$W(f,g):={\begin{bmatrix}f&g\\f'&g'\end{bmatrix}}=fg'-gf'$

Function is linearly independent if $W(f,g)\neq 0$

1) $f(x)=x,g(x)=x^{5}$

$f(x)=x,f'(x)=1$
$g(x)=x^{5},g'(x)=5x^{4}$
$W(f,g):={\begin{bmatrix}x&x^{5}\\1&5x^{4}\end{bmatrix}}=5x^{5}-x^{5}=4x^{5}\neq 0$ so function is linearly independent.

2) $f(x)=cos2x,g(x)=sin4x$

$f(x)=cos2x,f'(x)=-2sin2x$
$g(x)=sin4x,g'(x)=4cos4x$

$W(f,g):={\begin{bmatrix}cos2x&sin4x\\-2sin2x&4cos4x\end{bmatrix}}=cos2x*4cos4x+sin4x*2sin2x\neq 0$ so function is linearly independent.

Gramian:
$\Gamma (f,g):={\begin{bmatrix}<f,f>&<f,g>\\<g,f>&<g,g>\end{bmatrix}}$

Function is linearly independent if $\Gamma (f,g)\neq 0$

1) $f(x)=x,g(x)=x^{5}$
$<f,f>=\int _{-1}^{1}x^{2}dx={\frac {2}{3}}$
$<f,g>=\int _{-1}^{1}x^{6}dx={\frac {2}{7}}$
$<g,f>=\int _{-1}^{1}x^{6}dx={\frac {2}{7}}$
$<g,g>=\int _{-1}^{1}x^{1}0dx={\frac {2}{11}}$

$\Gamma (f,g):={\begin{bmatrix}{\frac {2}{3}}&{\frac {2}{7}}\\{\frac {2}{7}}&{\frac {2}{11}}\end{bmatrix}}\neq 0$ so function is linearly independent.

2) $f(x)=cos2x,g(x)=sin4x$
$<f,f>=\int _{-1}^{1}cos2x*cos2xdx={\frac {1}{4}}(4+sin4)=.818$
$<f,g>=\int _{-1}^{1}cos2x*sin4xdx=[.5cos^{2}x-1/12cos6x]_{-}^{1}1=0$
$<g,f>=\int _{-1}^{1}cos2x*sin4xdx=0$
$<g,g>=\int _{-1}^{1}sin4x*sin4xdx=1+{\frac {sin8}{8}}=.876$

$\Gamma (f,g):={\begin{bmatrix}.818&0\\0&.876\end{bmatrix}}\neq 0$ so function is linearly independent.

Honor Pledge

On our honor, we solved this problem on our own, without aid from online solutions or solutions from previous semesters.

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.