University of Florida/Egm4313/f13-team9-R1

Problem 1.1 (Pb-10.1 in sec.10.)

On our honor, we did this problem on our own, without looking at the solutions in previous semesters or other online solutions.

Problem Statement

Soultion

Step 1

Step 2

Step 3

Problem 1.2 (Sec. 1, Pb 1-2)

On our honor, we did this problem on our own, without looking at the solutions in previous semesters or other online solutions.

Problem Statement

Derive the equation of motion of the mass-spring-dashpot in Fig. 53 in K2011 p.85 with applied force r(t) on the ball.

Solution

Part (a): Determining torque in a hollow cylinder:

Part (b): Determining the maximum shearing stress in a solid cylinder:

Problem 1.3

Problem Statement

Given

Solution

Step One:

Problem 1.4 ( Sec. 2, Pb 2-1)

On our honor, we did this problem on our own, without looking at the solutions in previous semesters or other online solutions.

Problem Statement

Given

Solution

Step One:

Step Two:

Step Three:

Problem 1.5 ( P 2.2.5, P 2.2.12, Kreyszig, 2011)

On our honor, we did this problem on our own, without looking at the solutions in previous semesters or other online solutions.

Problem 2.2.5

Problem Statement

Solution

Part (a):

Part (b):

Problem 2.2.12

Problem Statement

Solve the initial value problem and graph the solution over the intervals $\displaystyle 0\leq x\leq 1\,,\,0\leq x\leq 5$

y''+9y'+20=0

(1)

Given

$\displaystyle y(0)=1$
$\displaystyle y'(0)={\frac {1}{2}}$

Solution

Step 1: Find a General Solution

The ODE is a linear, second-order, homogeneous differential equation with constant coefficients. So, the following equation was chosen as a solution.

y=e^{\lambda x}

(2)

The first and second derivatives are as follows:

y'=\lambda e^{\lambda x}

(3)

y''=\lambda ^{2}e^{\lambda x}

(4)

Plugging the solution and its derivatives back into the original ODE, we receive

(\lambda ^{2}+9\lambda +20)e^{\lambda x}=0

(5)

and the characteristic equation

\lambda ^{2}+9\lambda +20=0

(6)

This gives us 2 real solutions from the quadratic formula, $\displaystyle \lambda _{1}=-4\,,\,\lambda _{2}=-5$ and the general solution:

y=c_{1}e^{-4x}+c_{2}e^{-5x}

(7)

Step 2: Solve the IVP

Equation (7) and its derivative

y'=-4c_{1}e^{-4x}-5c_{2}e^{-5x}

(8)

can be set equal to the initial values given

y(0)=1=c_{1}+c_{2}

(9)

y'(0)={\frac {1}{2}}=-4c_{1}-5c_{2}

(10)

Solving (9) and (10) simultaneously gives us the c-values and the solution to the IVP

y=5.5e^{-4x}-4.5e^{-5x}

(11)

Step 3: Check Answer with Substitution

Our solution and its first two derivatives can be substituted into the original ODE

y''+8y'+20y=0

(12)

y=5.5e^{-4x}-4.5e^{-5x}

(13)

y'=-22e^{-4x}+22.5e^{-5x}

(14)

y''=88e^{-4x}-112.5e^{-5x}

(15)

[88+9(-22)+20(5.5)]e^{-4x}+[-112.5+9(22.5)+20(-4.5)]e^{-5x}=0

(16)

Which is true.

Step 4: Graph Solution

Graph over interval [0,1].

Graph over interval [0,5].

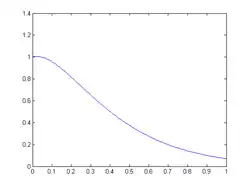
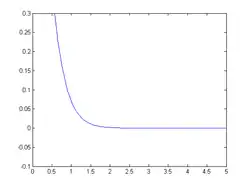
Problem 1.6 (P3.17, Beer2012)

On our honor, we did this problem on our own, without looking at the solutions in previous semesters or other online solutions.

Problem Statement

Solution

Step One:

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.