University of Florida/Egm4313/s12.team15.r2

Given

${\displaystyle \lambda _{1}=-2\!}$

${\displaystyle \lambda _{2}=+5\!}$

${\displaystyle y(0)=1\!}$

${\displaystyle y{}'(0)=0\!}$

${\displaystyle r(x)=0\!}$

Find

Find the non-homogeneous linear 2nd order ordinary differential equation with constant coefficients in standard form and the solution in terms of the initial conditions and the general excitation ${\displaystyle r(x)}$.

Then plot the solution.

Solution

Some of the following standard equations were referenced from the textbook Advanced Engineering Mechanics 10th Ed. Kreyszig 2011.

Standard Form:
${\displaystyle \lambda ^{2}+a\lambda +b=0\!}$

${\displaystyle (\lambda -\lambda _{1})(\lambda -\lambda _{2})=0\!}$

${\displaystyle \lambda ^{2}-\lambda \lambda _{2}-\lambda \lambda _{1}+\lambda _{1}\lambda _{2}=0\!}$

${\displaystyle \lambda ^{2}-5\lambda +2\lambda -10=0\!}$

${\displaystyle \lambda ^{2}-3\lambda -10=0\!}$

Therfore,
${\displaystyle a=-3\!}$

${\displaystyle b=-10\!}$

Standard Form:
${\displaystyle y{}''+ay{}'+by=r(x)=0\!}$

${\displaystyle y{}''-3y{}'-10y=0\!}$

Standard Form:
${\displaystyle y(x)=y_{h}(x)+y_{p}(x)\!}$

${\displaystyle y_{h}(x)=c_{1}e^{-2x}+c_{2}e^{5x}\!}$

${\displaystyle y_{p}(x)=0\!}$

Therefore,
${\displaystyle y_{p}{}'(x)=0\!}$

${\displaystyle y(x)=c_{1}e^{-2x}+c_{2}e^{5x}\!}$

${\displaystyle y{}'(x)=-2c_{1}e^{-2x}+5c_{2}e^{5x}\!}$

If
${\displaystyle y(0)=1\!}$

then
${\displaystyle 1=c_{1}e^{-2(0)}+c_{2}e^{5(0)}\!}$

${\displaystyle 1=c_{1}+c_{2}\!}$

If
${\displaystyle y{}'(0)=0\!}$

then
${\displaystyle 0=c_{1}e^{-2(0)}+c_{2}e^{5(0)}\!}$

${\displaystyle 0=c_{1}+c_{2}\!}$

${\displaystyle 2c_{1}=5c_{2}\!}$

${\displaystyle c_{1}={\frac {5}{2}}c_{2}\!}$

${\displaystyle 1={\frac {5}{2}}c_{2}+c_{2}\!}$

${\displaystyle 1={\frac {7}{2}}c_{2}\!}$

${\displaystyle c_{2}={\frac {2}{7}}\!}$

${\displaystyle 1=c_{1}+c_{2}\!}$

${\displaystyle c_{1}=1-c_{2}=1-{\frac {2}{7}}={\frac {5}{7}}\!}$

Final Solution:

${\displaystyle y(x)={\frac {5}{7}}e^{-2x}+{\frac {2}{7}}e^{5x}\!}$

Plot of Solution:

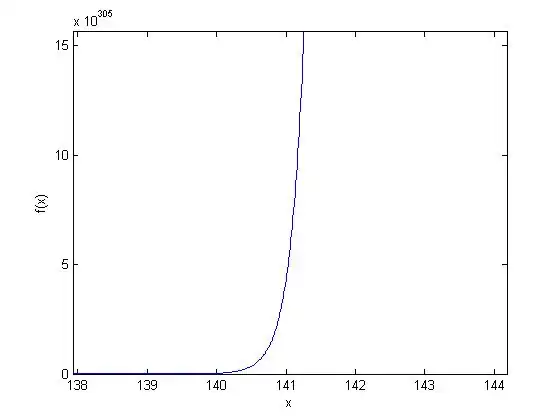
Author

Solved and typed by Kristin Howe
Reviewed By -

Given

Find

Solution

Author

Solved and typed by -
Reviewed By -

Given

3a) ${\displaystyle y{}''+6{}y'+8.96y=0\!}$

3b) ${\displaystyle y''+4y'+(\pi ^{2}+4)y=0\!}$

Find

Find the general solution of the ODEs.

Solution

3a)

${\displaystyle y{}''+6{}y'+8.96y=0\!}$

${\displaystyle a=6\!}$

${\displaystyle b=8.96\!}$

${\displaystyle \lambda ^{2}+a\lambda +b=0\!}$

${\displaystyle \lambda ^{2}+6\lambda +8.96=0\!}$

Using the quadratic formula:

${\displaystyle \lambda _{1/2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2}}\,\!}$ where ${\displaystyle \lambda _{1/2},\!}$ are the 2 different roots generated using quadratic formula.

Plug-in and solve using known variables (b=6, a=1, c=8.96)

${\displaystyle \lambda _{1/2}={\frac {-6\pm {\sqrt {0.16}}}{2}}\,\!}$ ${\displaystyle ={\frac {-6\pm 0.4}{2}}\,\!}$ ${\displaystyle =-3\pm 0.2\,\!}$

Therefore,

${\displaystyle \lambda _{1}=-2.8\,\!}$

${\displaystyle \lambda _{2}=-3.2\,\!}$

The General Solution formula for Distinct Real roots is
${\displaystyle y(x)=C_{1}e^{\lambda _{1}x}+C_{2}e^{\lambda _{2}x}}$

Now substitute the known roots into the General Solution formula:

  ${\displaystyle y(x)=C_{1}e^{-2.8x}+C_{2}e^{-3.2x}\!}$

Check using substitution. First, find the 1st and 2nd derivative of general solution formula:

${\displaystyle {y}'=-3.2C_{1}e^{-3.2x}-2.8C_{2}e^{-2.8x}\!}$

${\displaystyle {y}''=10.24C_{1}e^{-3.2x}+7.84C_{2}e^{-2.8x}\!}$

Then, plug in the known variables into the original equation:

${\displaystyle y{}''+6{}y'+8.96y=0\!}$ (Original Equation)

${\displaystyle 10.24c_{1}e^{-3.2x}+7.84c_{2}e^{-2.8x}-19.2c_{1}e^{-3.2x}-16.8c_{2}e^{-2.8x}+8.96c_{1}e^{-3.2x}+8.96c_{2}e^{-2.8x}=0\!}$

By inspection, all of the terms on the left side of the equation cancel out to 0, making the expression correct. Therefore, the general solution is correct.

3b)

${\displaystyle y''+4y'+(\pi ^{2}+4)y=0\!}$

${\displaystyle a=4\!}$

${\displaystyle b=(\pi ^{2}+4)\!}$

${\displaystyle \lambda ^{2}+a\lambda +b=0\!}$

${\displaystyle \lambda ^{2}+4\lambda +(\pi ^{2}+4)=0\!}$

Using the quadratic formula:

${\displaystyle \lambda _{1/2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2}}\,\!}$ where ${\displaystyle \lambda _{1/2},\!}$ are the 2 different roots generated using quadratic formula.

Plug-in and solve using known variables (b=4, a=1, c=[${\displaystyle \pi ^{2}}$ + 4])

${\displaystyle \lambda _{1/2}={\frac {-4\pm {\sqrt {-4\pi ^{2}}}}{2}}\,\!}$ ${\displaystyle ={\frac {-4\pm 2\pi i}{2}}\,\!}$ ${\displaystyle =-2\pm \pi i\,\!}$

Therefore,

${\displaystyle \lambda _{1}=-2+\pi i\,\!}$

${\displaystyle \lambda _{2}=-2-\pi i\,\!}$

The General Solution formula for Complex Conjugate roots is
${\displaystyle y(x)=e^{-{\frac {\alpha x}{2}}}(C_{1}\cos \beta x+C_{2}\sin \beta x)\!}$

Now substitute the known roots into the General Solution formula:

  ${\displaystyle y(x)=e^{-2x}(C_{1}\cos \pi x+C_{2}\sin \pi x)\!}$

Check using substitution. First, find the 1st and 2nd derivative of general solution formula:

${\displaystyle {y}'=e^{-2x}(-C_{1}\pi sin(\pi x)+C_{2}\pi cos(\pi x))-2e^{-2x}(C_{1}cos(\pi x)+C_{2}sin(\pi x))\!}$

${\displaystyle {y}''=e^{-2x}(-C_{1}\pi ^{2}cos(\pi x)-C_{2}\pi ^{2}sin(\pi x)+2C_{1}\pi sin(\pi x)-2C_{2}\pi sin(\pi x))-2e^{-2x}(-C_{1}\pi sin(\pi x)+C_{2}\pi cos(\pi x)-2C_{1}cos(\pi x)-2C_{2}sin(\pi x))\!}$

Then, plug in the known variables into the original equation:

${\displaystyle y''+4y'+(\pi ^{2}+4)y=0\!}$ (Original Equation)

${\displaystyle e^{-2x}(-C_{1}\pi ^{2}cos(\pi x)-C_{2}\pi ^{2}sin(\pi x)+2C_{1}\pi sin(\pi x)-2C_{2}\pi sin(\pi x))-2e^{-2x}(-C_{1}\pi sin(\pi x)+C_{2}\pi cos(\pi x)-2C_{1}cos(\pi x)-2C_{2}sin(\pi x))\!}$

${\displaystyle +4(e^{-2x}(-C_{1}\pi sin(\pi x)+C_{2}\pi cos(\pi x))-2e^{-2x}(C_{1}cos(\pi x)+C_{2}sin(\pi x)))\!}$

${\displaystyle +(\pi ^{2}+4)(e^{-2x}(C_{1}\cos \pi x+C_{2}\sin \pi x))=0\!}$

By inspection, all of the terms on the left side of the equation cancel out to 0, making the expression correct. Therefore, the general solution is correct.

Author

Solved and typed by - Tim Pham 19:36, 07 February 2012 (UTC)
Reviewed By -

Given

4a) ${\displaystyle y{}''+2\pi {}y'+\pi ^{2}y=0\!}$

4b) ${\displaystyle 10y{}''-32{}y'+25.6{}y=0\!}$

Find

Find the general solution. Check answer by substitution.

Solution

4a)

${\displaystyle y{}''+2\pi {}y'+\pi ^{2}y=0\!}$

${\displaystyle a=2\pi \!}$

${\displaystyle b=\pi ^{2}\!}$

${\displaystyle \lambda ^{2}+a\lambda +b=0\!}$

${\displaystyle \lambda ^{2}+2\pi \lambda +\pi ^{2}=0\!}$

Finding the roots:

${\displaystyle \lambda _{1}={\frac {1}{2}}(-2\pi +{\sqrt {(-2\pi )^{2}-4(\pi ^{2})}})=-\pi \!}$

${\displaystyle \lambda _{2}={\frac {1}{2}}(-2\pi -{\sqrt {(-2\pi )^{2}-4(\pi ^{2})}})=-\pi \!}$

Both solutions above show the double root characteristic so the following is applied:

${\displaystyle y_{1}=e^{-\pi {x}}\!}$

${\displaystyle y_{2}=uy_{1}\!}$

${\displaystyle u=c_{1}x+c_{2}\!}$ This is due to double integration.

So,

${\displaystyle y_{2}=(c_{1}x+c_{2})y_{1}\!}$

Choose ${\displaystyle c_{1}=1c_{2}=0\!}$

${\displaystyle y_{2}=(x+0)y_{1}\!}$

${\displaystyle y_{2}=xy_{1}\!}$

${\displaystyle y_{2}=xe^{-\pi {x}}\!}$

${\displaystyle y=(c_{1}+c_{2}x)e^{-\pi {x}}\!}$ General Solution

Check by substitution

${\displaystyle y=(c_{1}+c_{2}x)e^{-\pi {x}}\!}$

${\displaystyle y'=-\pi {}c_{1}e^{-\pi {x}}+c_{2}e^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}}\!}$

${\displaystyle y''=\pi ^{2}c_{1}e^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}}+\pi ^{2}c_{2}xe^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}}\!}$

${\displaystyle \pi ^{2}c_{1}e^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}}+\pi ^{2}c_{2}xe^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}}+2\pi {}(-\pi {}c_{1}e^{-\pi {x}}+c_{2}e^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}})+\pi ^{2}(e^{-\pi {x}}c_{1}+e^{-\pi {x}}xc_{2})=0\!}$

Since all terms cancel out then by substitution the general solution ${\displaystyle y=(c_{1}+c_{2}x)e^{-\pi {x}}\!}$ does hold true.

4b) ${\displaystyle 10y{}''-32{}y'+25.6{}y=0\!}$

Divide by 10 to simplify equation :

${\displaystyle y{}''-3.2{}y'+2.56{}y=0\!}$

${\displaystyle a=-3.2\!}$

${\displaystyle b=2.56\!}$

${\displaystyle \lambda ^{2}+a\lambda +b=0\!}$

${\displaystyle \lambda ^{2}-3.2\lambda +2.56=0\!}$

Solving for the roots:

${\displaystyle \lambda _{1}={\frac {1}{2}}(-(-3.2)+{\sqrt {(-3.2)^{2}-4(2.56)}})=1.6\!}$

${\displaystyle \lambda _{2}={\frac {1}{2}}(-(-3.2)-{\sqrt {(-3.2)^{2}-4(2.56)}})=1.6\!}$

${\displaystyle \lambda _{1}=\lambda _{2}\!}$ This shows the double root characteristic.

So, the following is applied

${\displaystyle y_{1}=e^{1.6x}\!}$

${\displaystyle y_{2}=uy_{1}\!}$

${\displaystyle u=c_{1}x+c_{2}\!}$ This is due to double integration

So

${\displaystyle y_{2}=(c_{1}x+c_{2})y_{1}\!}$

Choose ${\displaystyle c_{1}=1c_{2}=0\!}$

${\displaystyle y_{2}=(x+0)y_{1}\!}$

${\displaystyle y_{2}=xy_{1}\!}$

${\displaystyle y_{2}=xe^{1.6x}\!}$

${\displaystyle y=(c_{1}+c_{2}x)e^{1.6x}\!}$ General Solution

Check by Substitution

${\displaystyle y''=2.56c_{1}e^{1.6x}+1.6c_{2}e^{1.6x}+1.6c_{2}xe^{1.6x}+2.56c_{2}xe^{1.6x}\!}$

${\displaystyle y'=1.6c_{1}e^{1.6x}+c_{2}e^{1.6x}+1.6c_{2}xe^{1.6x}\!}$

${\displaystyle y=c_{1}e^{1.6x}+c_{2}xe^{1.6x}\!}$

${\displaystyle 10(2.56c_{1}e^{1.6x}+1.6c_{2}e^{1.6x}+1.6c_{2}xe^{1.6x}+2.56c_{2}xe^{1.6x})-32(1.6c_{1}e^{1.6x}+c_{2}e^{1.6x}+1.6c_{2}xe^{1.6x})+25.6(c_{1}e^{1.6x}+c_{2}xe^{1.6x})=0\!}$

Since all terms cancel out then through substitution it can be confirmed that the general solution

${\displaystyle y=(c_{1}+c_{2}x)e^{1.6x}\!}$ does hold true.

Author

Solved and typed by - Cynthia Hernandez
Reviewed By -

Given

Problem 16, P 59 Kreyszig:

${\displaystyle e^{2.6x},e^{-4.3x}\!}$

Problem 17, P 59 Kreyszig:

${\displaystyle e^{-{\sqrt {5}}x},xe^{-{\sqrt {5}}x}\!}$

Find

Problem 16, P 59 Kreyszig:

ODE in the form:

${\displaystyle {y}''+a{y}'+by=0\!}$

Problem 17, P 59 Kreyszig:

ODE in the form:

${\displaystyle {y}''+a{y}'+by=0\!}$

Solution

Problem 16, P 59 Kreyszig:

For two distinct real-roots:

${\displaystyle y=c_{1}e^{\lambda _{1}x}+c_{2}e^{\lambda _{2}x}\!}$

Where:

${\displaystyle \lambda _{1}=2.6\!}$ and ${\displaystyle \lambda _{2}=-4.3\!}$

The characteristic equation is:

${\displaystyle \lambda ^{2}+a\lambda +b=0\!}$

Multiplying the roots of the equation together:

${\displaystyle (\lambda -2.6)(\lambda +4.3)=\lambda ^{2}+1.7\lambda -11.18\!}$

Therefore the ODE is:

${\displaystyle y''+1.7y'-11.18y=0\!}$

Problem 17, P 59 Kreyszig:

For real double root:

${\displaystyle y=(c_{1}+c_{2}x)e^{\lambda x}\!}$

Where:

${\displaystyle \lambda =-{\sqrt {5}}\!}$

The characteristic equation is:

${\displaystyle \lambda ^{2}+a\lambda +b=0\!}$

Multiplying the roots of the equation together:

${\displaystyle (\lambda +{\sqrt {5}})^{2}=\lambda ^{2}+2{\sqrt {5}}\lambda +5\!}$

Therefore the ODE is:

${\displaystyle y''+2{\sqrt {5}}y'+5y=0\!}$

Author

Solved and typed by - Neil Tidwell 1:55, 06 February 2012 (UTC)
Reviewed By -

Given

Spring-Dashpot-Mass System from Sec 1 lecture notes.

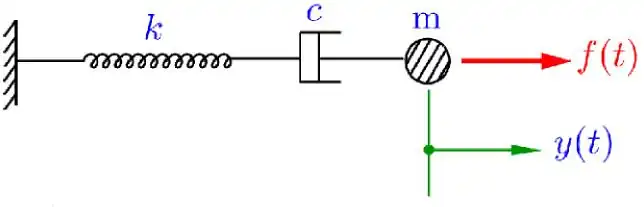
Has double real root ${\displaystyle \lambda =-3\!}$

Find

${\displaystyle k,c,m\!}$

Solution

For spring-mass-dashpot system:

${\displaystyle m(y_{k}''+{\frac {k}{c}}y_{k}')+ky_{k}=f(t)\!}$

This simplifies to:

${\displaystyle y_{k}''+{\frac {k}{mc}}y_{k}'+{\frac {k}{m}}y_{k}=f(t)\!}$

Multiply roots together to get characteristic equation:

${\displaystyle (\lambda +3)^{2}=\lambda ^{2}+6\lambda +9\!}$

Set coefficients of simplified spring-mass-dashpot equation equal to those of characteristic equation:

${\displaystyle {\frac {k}{mc}}=6\!}$

${\displaystyle {\frac {k}{m}}=9\!}$

Have one degree of freedom, so arbitrarily choose ${\displaystyle m=1\!}$

Solve system:

${\displaystyle m=1\!}$
${\displaystyle k=9\!}$
${\displaystyle c=1.5\!}$

Author

Solved and typed by - Neil Tidwell 2:14, 06 February 2012 (UTC)
Reviewed By -

Given

Develop the MacLaurin Series (Taylor Series at ${\displaystyle t=0\!}$) for ${\displaystyle e^{t},\cos t,\sin t\!}$

${\displaystyle L[y]andL[w]thenL[y+w]\!}$

${\displaystyle L[y+w]=L[y]+L[w]\!}$

${\displaystyle L[cy]=cL[y]}$

${\displaystyle L[kw]=kL[w]\!}$

Find

Solution

Author

Solved and typed by - Jenny Schulze
Reviewed By -

Given

Find a general solution to the equations, and check answers by substitution.

Problem 8

${\displaystyle y''+y'+3.25y=0\!}$

(8.0)

Problem 15

${\displaystyle y''+0.54y'+(0.0729+\pi )y=0\!}$

(8.1)

Find

Factor as in the text and solve.

Solution

Author

Solved and typed by - Jenny Schulze
Reviewed By -

Given

Initial Conditions:

${\displaystyle y(0)=1,y'(0)=0\ }$

No excitation:

${\displaystyle r(x)=0\ }$

Find

Find and plot the solution for the L2-ODE-CC corresponding to:

${\displaystyle \lambda ^{2}+4\lambda +13=0\!}$

In another Fig., superimpose 3 Figs.: (a) this Fig., (b) the Fig. in R2.6 p.5-6, (c) the Fig. in R2.1 p.3-7.

Solution

The corresponding ODE in standard form:

${\displaystyle y''+4y'+13y=r(x)\!}$

To find the roots of the ODE, convert ODE to this form:

${\displaystyle a\lambda ^{2}+b\lambda +c=0\!}$

which in this case is:

${\displaystyle \lambda ^{2}+4\lambda +13=0\!}$

use the formula to find the roots:

${\displaystyle \lambda _{1,2}={\frac {-b\pm i{\sqrt {b^{2}-4ac}}}{2a}}=-\alpha \pm i\omega }$

${\displaystyle \lambda _{1,2}={\frac {-4\pm i{\sqrt {4^{2}-4*1*13}}}{2*1}}=-2\pm 3i}$

because the roots are complex conjugates, the general solution can be given as:

${\displaystyle y(t)=e^{-\alpha t}(Acos\omega t+bsin\omega t)=e^{-2t}(Acos3t+Bsin3t)\!}$

to find A and B, we use the initial conditions and take the first derivative of y(t):

${\displaystyle y(0)=1=e^{-2*0}(Acos(3*0)+Bsin(3*0)=1*A=A\!}$

${\displaystyle A=1\!}$

${\displaystyle y'(t)=e^{-2t}((-2A+3B)cos(3t)-(3A+2B)sin(3t))\!}$

${\displaystyle y'(0)=0=e^{-2*0}((-2*1+3B)cos(3*0)-(3*1+2B)sin(3*0))=1*(-2+3B)=-2+3B\!}$

${\displaystyle B={\frac {2}{3}}\!}$

thus:

${\displaystyle y(t)=e^{-2t}(cos3t+{\frac {2}{3}}sin3t)\!}$

The graph of the solved equation is shown below in Fig. 1.

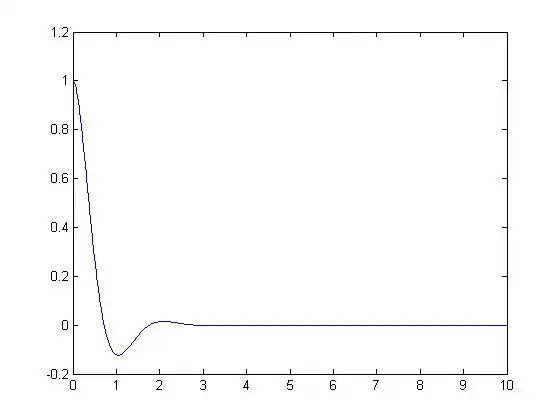
The three graphed equations are shown together below in Fig. 2

Equation 1 (R2.9):

${\displaystyle y_{1}(t)=e^{-2t}(cos3t+{\frac {2}{3}}sin3t)\!}$

Equation 2 (R2.6):

${\displaystyle y_{2}(t)=e^{-3t}+3te^{-3t}\!}$

Equation 3 (R2.1):

${\displaystyle y_{3}(t)={\frac {5}{7}}e^{-2t}+{\frac {2}{7}}e^{5t}\!}$

Author

Solved and typed by - --James Moncrief 01:42, 8 February 2012 (UTC)
Reviewed By -

Contributing Members