Why does potential-based reward shaping seem to alter the optimal policy in this case?

Question

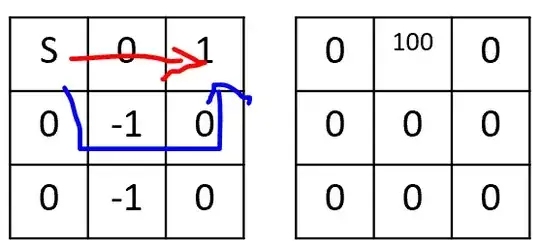
It is known that every potential function won't alter the optimal policy [1]. I lack of understanding why is that.

The definition:

$$R' = R + F,$$ with $$F = \gamma\Phi(s') - \Phi(s),$$

where, let's suppose, $\gamma = 0.9$.

If I have the following setup:

• on the left is my $R$.
• on the right my potential function $\Phi(s)$
• the top left is the start state, the top right is the goal state

The reward for the red route is: $(0 + (0.9 * 100 - 0)) + (1 + (0.9 * 0 - 100)) = -9$.

And the reward for the blue route is: $(-1 + 0) + (1 + 0) = 0$.

So, for me, it seems like the blue route is better than the optimal red route and thus the optimal policy changed. Do I have erroneous thoughts here?

Answer 1

The same $\gamma = 0.9$ that you use in the definition $F \doteq \gamma \Phi(s') - \Phi(s)$ should also be used as the discount factor in computing returns for multi-step trajectories. So, rather than simply adding up all the rewards for your different time-steps for the different trajectories, you should discount them by $\gamma$ for every time step that expires.

Therefore, the returns of the blue route are:

$$0 + (0.9 \times -1) + (0.9^2 \times 0) + (0.9^3 \times 1) = -0.9 + 0.729 = -0.171,$$

and the returns of the red route are:

$$(0 + 0.9 \times 100 - 0) + 0.9 \times (1 + 0.9 \times 0 - 100) = 90 - 89.1 = 0.9.$$