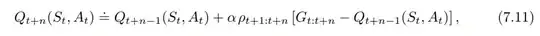5

In Sutton & Barto's book (2nd ed) page 149, there is the equation 7.11

enter image description here

I am having a hard time understanding this equation.

I would have thought that we should be moving $Q$ towards $G$, where $G$ would be corrected by importance sampling, but only $G$, not $G-Q$, therefore I would have thought that the correct equation would be of the form

$Q \leftarrow Q + \alpha (\rho G - Q)$

and not

$Q \leftarrow Q + \alpha \rho (G - Q)$

I don't get why the entire update is weighted by $\rho$ and not only the sampled return $G$.

nbro
  • 39,006
  • 12
  • 98
  • 176
Antoine Savine
  • 153
  • 4
  • Thank you @nbro for the edit, I was a bit lazy with the equations :) – Antoine Savine Apr 05 '19 at 14:30
  • Hi Antoine! Please, next time try to at least put some more effort to write these equations! Whenever I can, I try to write them nicely, but I would prefer if every user does it for its own questions/answers, of course! – nbro Apr 05 '19 at 14:31

1 Answers1

3

Multiplying the entire update by $\rho$ has the desirable property that experience affects $Q$ less when the behavior policy is unrelated to the target policy. In the extreme, if the trajectory taken has zero probability under the target policy, then $Q$ isn't updated at all, which is good. Alternatively, if only $G$ is scaled by $\rho$, taking zero probability trajectories would artificially drive $Q$ to zero.

Philip Raeisghasem
  • 2,028
  • 9
  • 29