Previously I have learned that the softmax as the output layer coupled with the log-likelihood cost function (the same as the the nll_loss in pytorch) can solve the learning slowdown problem.
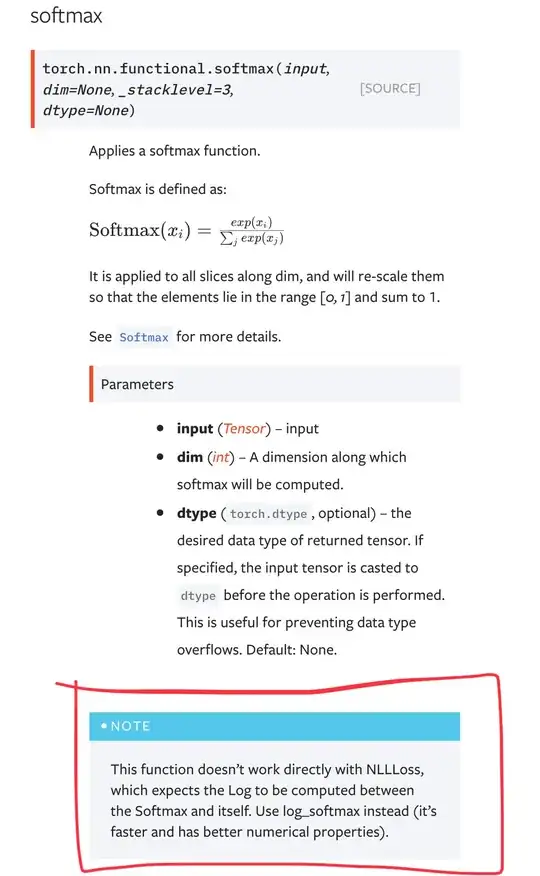
However, while I am learning the pytorch mnist tutorial, I'm confused that why the combination of the log_softmax as the output layer and the nll_loss(the negative log likelihood loss) as the loss function was used (L26 and L34).
I found that when log_softmax+nll_loss was used, the test accuracy was 99%, while when softmax+nll_loss was used, the test accuracy was 97%.
I'm confused that what's the advantage of log_softmax over softmax? How can we explain the performance gap between them? Is log_softmax+nll_loss always better than softmax+nll_loss?