10

Why don't people use nonlinear activation functions after projecting the query key value in attention?

It seems like doing this would lead to much-needed nonlinearity, otherwise, we're just doing linear transformations.

This observation applies to the transformer, additive attention, etc.

nbro
  • 39,006
  • 12
  • 98
  • 176
user3180
  • 598
  • 3
  • 14
  • 1
    Can you provide an example of someone not using nonlinear activations in their attention? – Philip Raeisghasem May 04 '19 at 21:53
  • I'm not sure if I got your question right, for the attention model where exactly would you place the non-linearity? Looking at [Graph Attention Networks](https://arxiv.org/pdf/1710.10903.pdf) by Petar Velickovic, they do apply an activation function in eq. 5. – razvanc92 May 03 '19 at 07:21
  • 2
    I think what he means is that the queries, keys and values are computed as linear projections, i.e. the input is simply multiplied by a matrix, `q = x * W_q`, `k = x * W_k` and `v = x * W_v` respectively. We could use a non-linear function on each of them, `q = σ(x * W_q)` etc., but it is redundant because later on we use the softmax function and at the end a MLP which also has non-linearities in it. – Andreas K. Jul 23 '22 at 08:13

1 Answers1

4

It seems like doing this would lead to much-needed nonlinearity, otherwise, we're just doing linear transformations.

Attention is broadly defined as a following operation ($\text{softmax}$ is sometimes replaced by $\tanh$) :

$$\text{Attention}(Q,K,V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V $$

Where $Q$, $K$ and $V$ are matrices that are some functions of the inputs.
There are three nonlinear operations there:

  1. The inner projection $QK^T$ is nonlinear. We have multiplication of two functions of the inputs. For example, in case of self-attention $Q=X W_Q$ and $K = XW_K$ are two linear transforms of the same $X$, so $QK^T = X \left(W_Q W_K^T\right) X^T$ is a quadratic function of the inputs.
  2. The $\text{softmax}(x_i) = e^{x_i} /\sum_n e^{x_n} $ function is obviously nonlinear ($\tanh$ as well)
  3. The final $\text{softmax}(\dots) V$ product is also nonlinear for the same reasons as (1)

I would say that it is pretty clear that it is definitely not just a linear transformation - there's quite a lot of nonlinearities in the attention block.

This observation applies to the transformer, additive attention, etc.

Let's see what happens next with the outputs of the attention layers:

In the transformer model, outputs of the multi-head-self-attention are fed into a feed-forward network inside each block:

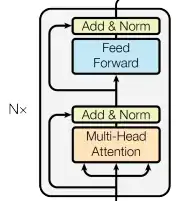
Transformer figure1 cutout

"Feed-forward" means that the inputs are multiplied by a weight matrix and then a nonlinear activation function is applied.

The additive attention approach, directly applies another $\text{softmax}$ on the outputs of what one would call the attention block:

$$e_{ij} = v_a^T \tanh\left(W_as_{i-1} + U_a h_j\right)$$

$$\alpha_{ij} = \frac{\exp(e_{ij})}{\sum_k \exp(e_{ik})}$$

To summarize - I don't think that the premise of the question is correct. Various nonlinearities are present both inside the attention blocks and, typically, are applied after the attention is computed.

Kostya
  • 2,416
  • 7
  • 23
  • Self attention does not meat that $Q = K = X$. It only means that $Q=XW_Q$ and $K=XW_K$ or in other words that K and Q are obtained from the same X, as opposed to cross-attention where keys and queries come from different sequences. – hans Mar 11 '23 at 23:51
  • @hans I stand corrected, thank you. Edited the answer to reflect that – Kostya Mar 12 '23 at 13:33