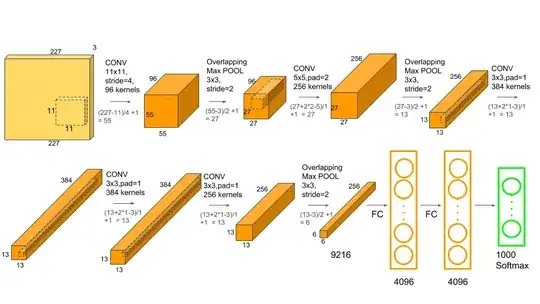
Consider AlexNet, which has 1000 output nodes, each of which classifies an image:
The problem I have been having with training a neural network of similar proportions, is that it does what any reasonable network would do: it finds the easiest way to reduce the error which happens to be setting all nodes to 0, as in the vast majority of the time, that's what they'll be. I don't understand how a network where 999 times out of 1000, the node's output is 0, could possibly learn to make that node 1.
But obviously, it's possible, as AlexNet did very well in the 2012 ImageNet challenge. So I wanted to know, how would one train a neural network (specifically a CNN) when for the majority of the inputs the desired value for an output node is 0?