1

I was watching a video about Convolutional Neural Networks: https://www.youtube.com/watch?v=SQ67NBCLV98. What I'm confused about is the arrangement of applying the filters' channels to the input image or even to the output of a previous layer.

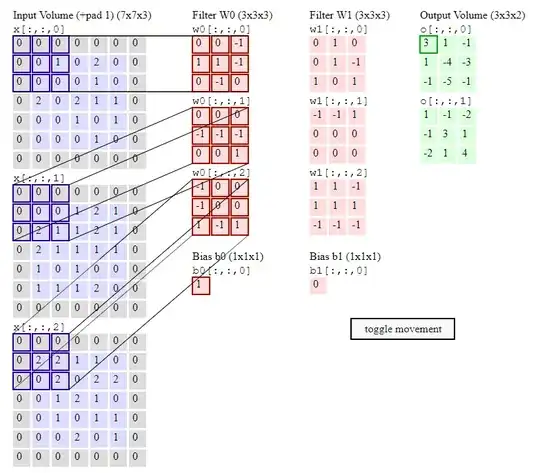
Question 1 - Looking at the visual explanation example of how one filter with 3 channels is applied to the input image (with 3 channels), so that each 1 filter channel is applied to its corresponding input channel: 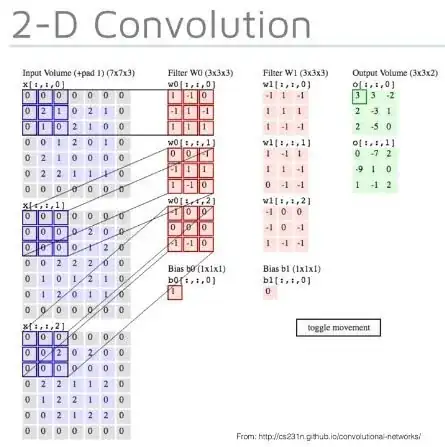Conv 2_D. So hence the output is 3 channels. Makes sense.

However, looking at the second screenshot which shows an example of the VGG network: 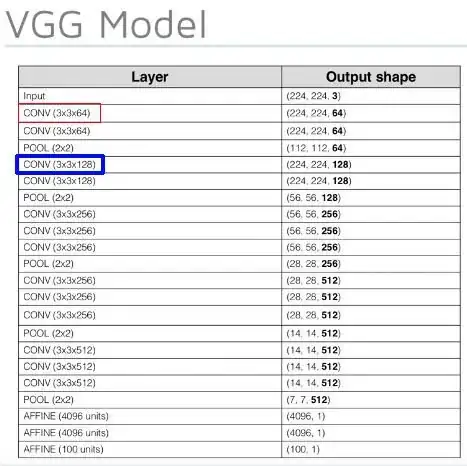VGG, looking at the first layer (I've delineated with a red frame), which is 64 channels, where the input of the image contains 3 channels. How does the output shape become 64? The only way I would think this would be possible is if you apply:

  • filter channel 1 to image channel 1
  • filter channel 2 to image channel 2
  • filter channel 3 to image channel 3
  • filter channel 4 to image channel 1
  • filter channel 5 to image channel 2
  • filter channel 6 to image channel 3

.. and so on.

Or the other thing could be, that these are representing Conv layers, with 64 filters. Rather than a filter with 64 channels. And that's precisely what I'm confused about here. In all the popular Convolutional networks, when we see these big numbers - 64, 128, 256 ... etc, are these Conv layers with 64 filters, or are they individual filters with 64 channels each?

Question 2 - Referring back to the second screenshot, the layer I've delineated with blue frame (3x3x128). This Conv layer, as I understand, takes the output of 64 Max-pooled nodes and applies 128 Conv filters. But how does the output become 128. If we apply each filter to each Max-pooled output node, that's 64 x 128 = 8192 channels or nodes in output shape. Clearly that's not what's happening and so I'm definitely missing something here. So, how does 128 filters is applied to 64 output nodes in a way so that the output is still 128? What's the arrangement?

Many thanks in advance.

Community
  • 1
Hazzaldo
  • 279
  • 2
  • 9

1 Answers1

1

Ok, here's the break down:

The depth of an input to a convolutional layer is termed channels. The depth of a convolutional layer is the number of kernels (aka filters). The depth of a kernel is equal to the number of channels in the input.

See below:

Convolution

The input (of 7x7, pad of 1) has 3 channels. The convolutional layer has 2 kernels (or filters). Each filter has a depth of 3, equal to the number of channels in the input. Using the notation you used in your question:

  • Filter 1, channel 1 to input channel 1
  • Filter 1, channel 2 to input channel 2
  • Filter 1, channel 3 to input channel 3

  • Sum all three channels of filter 1, then add bias

  • Filter 2, channel 1 to input channel 1

  • Filter 2, channel 2 to input channel 2
  • Filter 2, channel 3 to input channel 3
  • Sum all three channels of filter 2, then add bias

These steps are repeated for each frame the filter slides over the input image.

To answer question 2, if the output is 128, that simply means there are 128 filters. There could be an infinite number of filters if you so choose.

EDIT:

Here's the link to the interactive graphic: http://cs231n.github.io/convolutional-networks/

Recessive
  • 1,346
  • 8
  • 21
  • Apologies for the late reply. Thank you v much for the answer. Makes sense. With regards to question 2, I may have not phrased the question clearly. My question was how do you apply 128 filters to 64 outputs from Maxpool layer, and still end up with an output of 128 feature maps. My thought was, each filter is applied to each Maxpool output. In this case you end up with 64 x 128 filters = 8192 feature maps instead of 128. However, when I read the article your shared: http://cs231n.github.io/convolutional-networks/, in the entire article there's one key sentence which I think helps explain .. – Hazzaldo Jul 30 '19 at 19:32
  • “As we will soon see, the neurons in a layer will only be connected to a small region of the layer before it, instead of all of the neurons in a fully-connected manner”. So my thinking/understanding of this (which I could be wrong), is that only a select outputs will have a select filters applied to them in such a way where you end up with the same number of output feature maps as the filters. In the case of the 64 “Maxpooled” outputs, perhaps every 1 Maxpool output is connected to 2 filters ... – Hazzaldo Jul 30 '19 at 19:33
  • which makes sense because then you would get the output of 128 feature maps. Does that make sense and is it correct? – Hazzaldo Jul 30 '19 at 19:33
  • Not quite, but you're on the right idea. I think what's confusing is the term "filter", which I would argue is horrifically incorrect, as a "filter", is actually rather a collection of filters (called channels). So in this case, the 128 filters are each a collection of 64 filters (channels), which correspond to a depth level of the output of the maxpool layer. – Recessive Jul 31 '19 at 01:27
  • Say we're filter collection 1, then we perform the intuitive sliding and multiplying of each of the 64 filters (channels) in the collection, then for each output node of the collection, take the total sum of all 64 filters (channels) at that location, and then once put through an activation function, that is your final output for that layer. – Recessive Jul 31 '19 at 01:27
  • Excellent explanation. That makes perfect sense now. So the key missing part of information that cleared it up for me is: "then for each output node of the collection, take the total sum of all 64 filters (channels) at that location". Man seriously, it's these small details that I found hard to clarify from literature and articles, or it's explained at the input image convolution layer stage, but I failed to apply the same concept from a Maxpool to another Convolution layer stage. Thank you very much. – Hazzaldo Jul 31 '19 at 17:59
  • 1
    I assumed the 64 channels of a filter collection start as aribitrary values that are optimised over time with the backpropagation optimisation gradient descent stage, much like the other parameters that get optimised in the network during the learning process. – Hazzaldo Jul 31 '19 at 18:01
  • Also one final question, how did you embed the screenshots in your thread so they appear in the post. Mine didn't show on the post, and you have to click on the image link to show it. :( – Hazzaldo Jul 31 '19 at 18:03
  • I just copied the image across rather then a link. Also just as a note, the initial values of the filters are always randomly selected, but over a specific range. You'll notice very quickly if you don't select the correct initial values the network will fail to learn almost every time, as you will get both exploding and vanishing numbers in the forward *and* backward pass. I asked a question in relation to this and got a fantastic answer, see here: https://ai.stackexchange.com/questions/13106/how-are-exploding-numbers-in-a-forward-pass-of-a-cnn-combated – Recessive Aug 01 '19 at 03:27
  • Many thanks for sharing :) – Hazzaldo Aug 02 '19 at 01:37
  • Sorry for asking another question, just one more question. You mentioned: "... take the total sum of all 64 filters (channels) at that location ...". Do we actually add all 64 matrices together, or do we get their combined 'dot' products? Also the final output should be only 1 matrix (feature map), correct? That way with every filter (and its 64 channels) produce only 1 output matrix(feature map), then we would have the expected 128 matrices (or 128 feature maps) output. – Hazzaldo Aug 04 '19 at 20:01
  • If you consider the output to be a 3d matrix, then yes, otherwise no, the output should be 128 2d matrices. Yes, you add the matrices together. – Recessive Aug 06 '19 at 06:44
  • Awesome, many thanks. – Hazzaldo Aug 07 '19 at 00:58