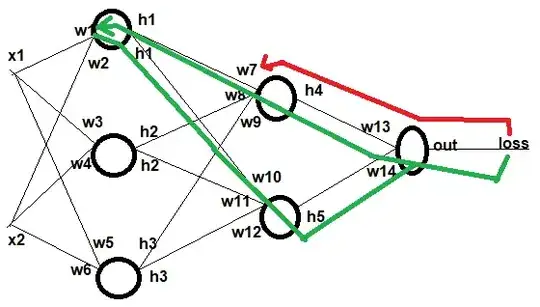
I'm trying to solve dLoss/dW1. The network is as in picture below with identity activation at all neurons:
Solving dLoss/dW7 is simple as there's only 1 way to output:
$Delta = Out-Y$
$Loss = abs(Delta)$
The case when Delta>=0, partial derivative of Loss over W7 is:
$\dfrac{dLoss}{dW_7} = \dfrac{dLoss}{dOut} \times \dfrac{dOut}{dH_4} \times \dfrac{dH_4}{dW_7} \\ = \dfrac{d(Out-Y)}{dOut} \times \dfrac{d(H_4W_{13} + H_5W_{14})}{dH_4} \times \dfrac{d(H_1W_7 + H_2W_8 + H_3W_9)}{dW_7} \\ = 1 \times W_{13} \times H_1$
However, when solving dLoss/dW1, the situation is very different, there are 2 chains to W1 through W7 and W10, and now, how should the chain for $\dfrac{dLoss}{dW_1}$ be?
Furthermore, at an arbitrary layer, with all outputs of all layers already calculated plus all gradients of weights on the right side also calculated, what should a formula for $\dfrac{dLoss}{dW}$ be?