I recently read a new paper (late 2019) about a one-shot object detector called CenterNet. Apart from this, I'm using Yolo (V3) one-shot detector, and what surprised me is the close similarity between Yolo V1 and CenterNet.
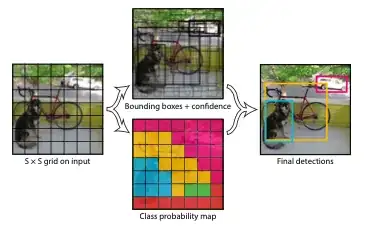
First, both frameworks treat object detection as a regression problem, each of them outputs a tensor that can be seen as a grid with cells (below is an example of an output grid).
Each cell in this grid predicts an object class, a box offset relative to the cell's position and a box size. The only major difference between Yolo V1 and CenterNet is that Yolo also predicts an object confidence score, that is represented in CenterNet by the class score. Yolo also predicts 2 boxes.
In brief, the tensor at one cell position is Class + B x (Conf + Size + Off) for Yolo V1 and Class + Size + Off for CenterNet.
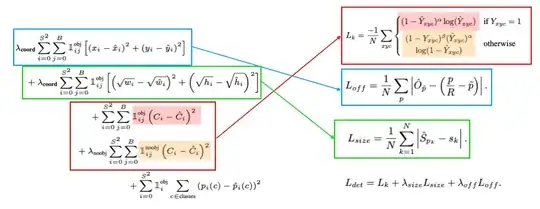
The training strategy is quite similar too. Only the cell containing the center of a ground truth is responsible for that detection and thus affects the loss. Cells near the ground truths center (base on the distance for CenterNet and IoU for Darknet) have a reduced penalty in the loss (Focal Loss for CenterNet vs and tuned hyper parameter for Yolo).
The loss functions have near the same structure (see above) except that L1 is preferred in CenterNet while Yolo uses L2, among other subtleties.
My point is not that Yolo V1 and CenterNet are the same — there are not — but they are far closer that it appears at first glance.
The problem is that recent papers like CenterNet (CornerNet, ExtremeNet, Triplet CenterNet, MatrixNet) all claim to be "Keypoint-based detector" while they are not so much different than regular "anchor-based" detectors (that are preconditioned regressors in fact).
Instead I think that the biggest difference between Yolo and CenterNet is the backbone that has a bigger resolution for CenterNet (64x64) while Darknet has 7 or 8 only.
My Question is: do you see a major difference between the two concepts that I may have missed and that could explain the performance gap? I understand that new backbones, new loss functions and better resolutions can improve the accuracy but is there a structural difference between the two approaches?