I am new to machine learning. I am reading this blog post on the VC dimension.
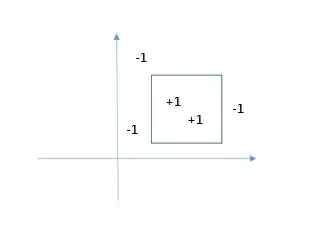
$\mathcal H$ consists of all hypotheses in two dimensions $h: R^2 → \{−1, +1 \}$, positive inside some square boxes and negative elsewhere.
An example.
My questions:
What is the maximum number of dichotomies for the 4 data points? i.e calculate mH(4)
It seems that the square can shatter 3 points but not 4 points. The $\mathcal V \mathcal C$ VC dimension of a square is 3. What is the proof behind this?