Can we get the inverse of the function that a neural network represents?

Question

I was wondering if it's possible to get the inverse of a neural network. If we view a NN as a function, can we obtain its inverse?

I tried to build a simple MNIST architecture, with the input of (784,) and output of (10,), train it to reach good accuracy, and then inverse the predicted value to try and get back the input - but the results were nowhere near what I started with. (I used the pseudo-inverse for the W matrix.)

My NN is basically the following function:

$$ f(x) = \theta(xW + b), \;\;\;\;\; \theta(z) = \frac{1}{1+e^{-z}} $$

I.e.

def rev_sigmoid(y):
    return np.log(y/(1-y))

def rev_linear(z, W, b):
    return (z - b) @ np.linalg.pinv(W)

y = model.predict(x_train[0:1])
z = rev_sigmoid(y)
x = rev_linear(z, W, b)
x = x.reshape(28, 28)
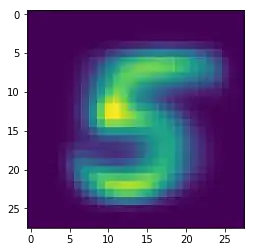
plt.imshow(x)

^ This should have been a 5:

Is there a reason why it failed? And is it ever possible to get inverse of NN's?

EDIT: it is also worth noting that doing the opposite does yield good results. I.e. starting with the y's (a 1-hot encoding of the digits) and using it to predict the image (an array of 784 bytes) using the same architecture: input (10,) and output (784,) with a sigmoid. This is not exactly equivalent, to an inverse as here you first do the linear transformation and then the non-linear. While in an inverse you would first do (well, undo) the non-linear, and then do (undo) the linear. I.e. the claim that the 784x10 matrix is collapsing too much information seems a bit odd to me, as there does exist a 10x784 matrix that can reproduce enough of that information.

Answer 1

Mathematical Exploration

let $\Theta^+$ be the pseudo-inverse of $\Theta$.

Recall, that if a vector $\boldsymbol v \in R(\Theta)$ (ie in the row space) then $\boldsymbol v = \Theta^+\Theta\boldsymbol v$. That is, so long as we select a vector that is in the rowspace of $\Theta$ then we can reconstruct it with full fidelity using the pseudo inverse. Thus, if any of the images happen to be linear combinations of the rows of $\Theta$ then we can reconstruct it.

To be more specific. let $f(\boldsymbol x)$ have a pseudo-inverse $f^+(\boldsymbol x)$ defined as you have. If we restrict our domain such that $\boldsymbol x \in C(\Theta^T)$ (column space of the transpose) then $f^+= f^{-1}_{res}$.

That is, under our domain restriction the pseudo inverse becomes a true inverse.

An Extrapolation

It would then seem that so long as we are under such domain restrictions then we could define a pseudo inverse for a general NN. Though, it might be possible that some NNs don't have any restriction that admits an inverse. Maybe, there is some way to regularize the parameters such that this is possible. NNs with ReLU wouldn't admit such an inverse since ReLU loses information on negative values. Leaky Relu might work.

Further Investigation

Finally, this presents a zone for further study. Some questions to answer might be:

• Is it possible for optimized parameters to contain non-trivial examples in their row-space?
• If so, under what conditions is this possible?
• Are the examples in any way represented in the row space?
• Is there some way to regularize a NN such that it admits an inverse over some desired restriction?
• Under what conditions is invertibility useful?

Answer 2

So, if I go the opposite way, start with my y and predict an x, and then ask for the inverse of that - I get really good results (actually - 100% accuracy).

i.e.

model = Sequential([
    Dense(784, input_shape=(10,), activation='sigmoid'),
])
model.compile(loss=keras.losses.binary_crossentropy,
              optimizer=keras.optimizers.Adam(0.01),
              metrics=['binary_crossentropy'])
model.fit(y_train, x_train,
          batch_size=batch_size,
          epochs=epochs,
          verbose=1,
          validation_data=(y_test, x_test))
# train until accuracy > 0.9, then:
W, b = model.get_weights()
y = y_train
x = reverse.predict(y)
z = rev_sigmoid(x)
y_hat = rev_linear(z, W, b)
(y_hat.argmax(axis=1) == y.argmax(axis=1)).mean()  # 1.0

After playing a bit with some toy examples, I think the other way is probably not possible, as the matrices don't have an inverse. Putting these (toy) matrices in WolframAlpha for example tells you the determinant is 0, but in numpy the determinant is just slightly bigger than 0, so you manage to calculate an "inverse" which is not really an inverse and get the bad results.

It's also makes sense. In the reversed scenario, we start with 10 dimension, expand to 784, and then collapse back to 10. But in the "regular" scenario, we start at 784, collapse to 10, and then expand to 784 again - and (I guess) too much information is lost then.

Answer 3

TL DR; I do not think the inverse of any reasonable neural network would exist.

Assume that you are using $32-bit$ floating-point numbers in the MNIST example. The number of distinct numbers that a $32-bit$ float can represent is finite (say $x$)

The number of different images you can put into the neural network = $x^{784}$. But the total number of distinct outputs is only $x^{10}$ (As the output is a vector of length $10$).

Hence by the pigeonhole principle there are multiple inputs that correspond to the same output.

Also on an average there are $x^{784}$ / $x^{10}$ = $x ^ {774}$ input images for a single output vector.

This means the function is not invertible as it is not one to one (and that by a long shot).

Some people are also discussing pseudo inverses. I do not know much about pseudo inverses. Still, for these to work (by that, I mean to be able to produce images of numbers from a given output vector), they should be able to distinguish between the $x ^ {774}$ images into

1. Images that look like real numbers and
2. Others, which are a total mess of flickering pixels that just happen to produce the given output.

Whatever algorithm solves this problem hence mush possesses domain knowledge of the problem, probably inherited through the neural network weights.

This seems to be an unexplored region of Neural Networks.

Hope this helps:)