5

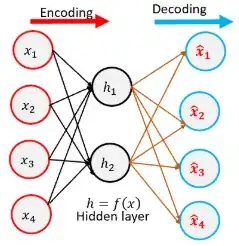
Given a pre-trained CNN model, I extract feature vector of images in reference and query dataset with several thousands of elements.

I would like to apply some augmentation techniques to reduce the feature vector dimension to speed up cosine similarity/euclidean distance matrix calculation.

I have already come up with the following two methods in my literature review:

  1. Principal Component Analysis (PCA) + Whitening
  2. Locality Search Hashing (LSH)

Are there more approaches to perform dimensionality reduction of feature vectors? If so, what are the pros/cons of each perhaps?

nbro
  • 39,006
  • 12
  • 98
  • 176
Farid Alijani
  • 299
  • 3
  • 10

2 Answers2

4

Dimensionality reduction could be achieved by using an Autoencoder Network, which learns a representation (or Encoding) for the input data. While training, the reduction side (Encoder) reduces the data to a lower-dimension and a reconstructing side (Decoder) tries to reconstruct the original input from the intermediate reduced encoding.

You could assign the encoder layer output ($L_i$) to a desired dimension (lower than that of the input). Once trained, $L_i$ could be used as a alternative representation of your input data in a lower feature-space, and can be used for further computations.

Autoencoder Architecture

s_bh
  • 360
  • 1
  • 5
  • 1
    Maybe this answer could be further improved if you link to a paper or implementation that shows the application of AE to reduce the dimensionality of feature vectors. If you consider images feature vectors, then, in a way, AE are commonly applied to reduce the dimensionality of images (or feature vectors), but what if the inputs are not images? – nbro Jan 26 '20 at 23:28
  • Is there any python library perform autoencoder efficiently? – Farid Alijani Feb 03 '20 at 06:44
  • 1
    @FäridAlijani Not that I know of. However, designing one in Keras wouldn't be much of a task. The following Keras blog might help : https://blog.keras.io/building-autoencoders-in-keras.html – s_bh Feb 03 '20 at 21:18
2

Some examples of dimensionality reduction techniques:

Linear methods Non-linear methods Graph-based methods
("Network embedding")
PCA
CCA
ICA
SVD
LDA
NMF		 Kernel PCA
GDA
Autoencoders
t-SNE
UMAP
MVU		 Diffusion maps
Graph Autoencoders

Graph-based kernel PCA
(Isomap, LLE, Hessian LLE, Laplacian Eigenmaps)

Though there are many more.

brazofuerte
  • 991
  • 8
  • 24