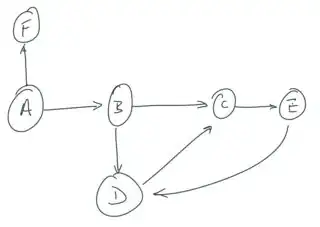
- It's not possible, as in the chain illustrated there are no transitions between A and C, C and D, and D and F. Only sequences where transitions exist are possible. The choice of transitions is arbitrary; it depends on what you want to model with it.
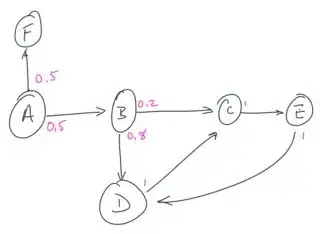
As DuttaA says in his comment, you can imagine that all nodes are linked with all other nodes, but those links have a transition probability of 0.0; so the probability of observing the sequence ACDF is actually 0.0 as well. In order to make the diagram more easy to understand, zero-probability transitions are generally not shown.
- There is no prescribed method of populating the transition probabilities. You can define the probabilities manually, randomly, or however you like. You could derive them from observable training data.
Re updating: this depends on the application. If you are modelling a process with known probabilities, you would not update the probabilities; if you are modelling a dynamic process which changes over time, then this is something you might want to consider. However, from my own experience (HMMs in speech recognition), once they have been assigned, they are generally kept as they are.
A Markov chain is really a fairly basic model; it gets more complex with a Hidden Markov Model, where you would generally use a learning algorithm to assign the transition and emission probabilities.