In Reinforcement Learning, an MDP model incorporates the Markovian property. A lot of scheduling applications in a lot of disciplines use reinforcement learning (mostly deep RL) to learn scheduling decisions. For example, the paper Learning Scheduling Algorithms for Data Processing Clusters, which is from SIGCOMM 2019, uses Reinforcement Learning for scheduling.
Isn't scheduling a non-Markovian process, or am I missing some points?
Lot of real tasks are in reality not markovian, but it doesn't mean you can't try to train an agent on these tasks. It's like saying "we assume variable x to be normally distributed", you just assume that you can condition the probability distributions on the present state of the environment hoping that the agent will learn a good policy. In fact for most applications the challenge is to frame a problem in order to make it as most plausibly markovian as possible (by compressing some important past information into a present state of the environment).
It is pretty common to just give for granted the Markov property, for example in NLP hidden Markov Models are used a lot for sequential tasks like entities detection, this of course leads to well known issues like high error rate on long sentences (the more you look into the future the more the error rate).
Note also that a Markov model can be of first order (probabilities conditioned only on the present state):
$P(W_{t+1} = w | W_{t}, W_{t-1},W_{t-2} ..) = P(W_{t+1} = w | W_{t})$
but they can also be of higher orders (for example second order if conditioning on the present state plus one step in the past):
$P(W_{t+1} = w | W_{t}, W_{t-1},W_{t-n} ..) = P(W_{t+1} = w | W_{t},W_{t-1})$
Of course the more steps in the past you condition the more quickly the problem becomes intractable, that's why almost always first order models are used.
EDIT
I add some comments on the scheduling paper as suggested by nbro.
So, here I would say that the most stryking aspect that makes the process look impossible to describe as an MDP is the presence of dependencies between jobs. Since I might need the result of certain jobs1 before to process another certain job2, there is surely no way that a time step t could be independent on time step t-1 (I need to know which job I processed in order to know which processes I can process or not).
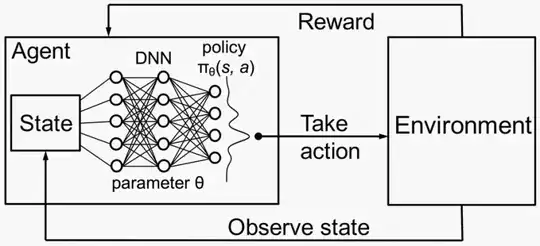
Here, the trick they use is to learn these dependencies between jobs thanks to a graph network, represented by the DNN in the deep reinforcement learning framework. So, what the agent has to learn is to select a tuple of two actions: "which output (i) a stage designated to be scheduled next, and (ii) an upper limit on the number of executors to use for that stage’s job". The information used to make this selection is the deep representation computed by the graph network on the decency graph of the jobs to schedule. In this sense, since the network is able to represent the 'temporal' relationships between jobs in the present state, this allows to assume that the choice of the next action tuple do not depend on previous states. Hope this is useful and make some sense to you.
