Well, GD terminates once the gradients are 0, right? Now, in a non-convex function, there could be some points, which do not belong to the global minima, and yet, have 0 gradients. For example, such points can belong to saddle points and local minima.
Consider this picture and say you start GD at the x label.
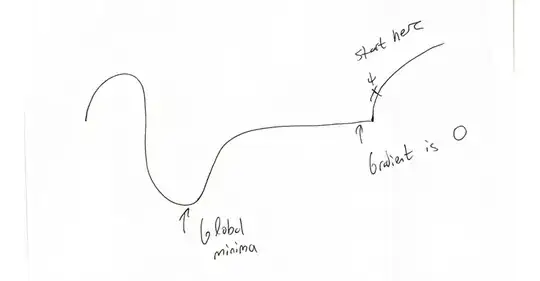
GD will bring you the flat area and will stop making progress there as gradients are 0. However, as you can see, global minima is to the left of this flat region.
By the same token, you have to show, for your own function, that there exists at least a single point whose gradients are 0 and yet, it is not the global minima.
In addition to that, the guarantee on converge for convex functions depends on annealing the learning rate appropriately. For example, if your LR is too high, GD can just keep overshooting the minima. The visualization from this page might help you to understand more regarding the behavior of GD.
