I'm trying to train a Policy Gradient Agent with Baseline for my RL research. I'm using the in-built RL toolbox from MATLAB (https://www.mathworks.com/help/reinforcement-learning/ug/pg-agents.html) and have created my own Environment. The goal is to train the system to sample an underlying time-series ($x$) given battery constrains ($\epsilon$ is battery cost).
The general setup is as follows:
- My Environment is a "sensor" system with exogenous input time-series and battery level as my States/Observations (size is 13x1).
- Actions $A_t$ are binary: 0 = keep a model prediction $(\hat x)$; 1 = sampling time series $(x)$
- Reward function is
$$ R = -[err(\tilde x, x) + A_t\cdot \epsilon ] + (-100)\cdot T_1 + (100) \cdot T_2 $$
where $err(\tilde x, x)$ is the RMSE error between the sampled time series $(\tilde x)$, and true time series x.
The Terminal State Rewards are -100 if sensor runs out of battery $T_1$ or 100 if reached the end of the episode with RMSE < threshold and remaining battery level $(T_2)$. The goal is to always end in $T_2$.
Each training Episode consists of a time-series of random length, and random initial battery level.
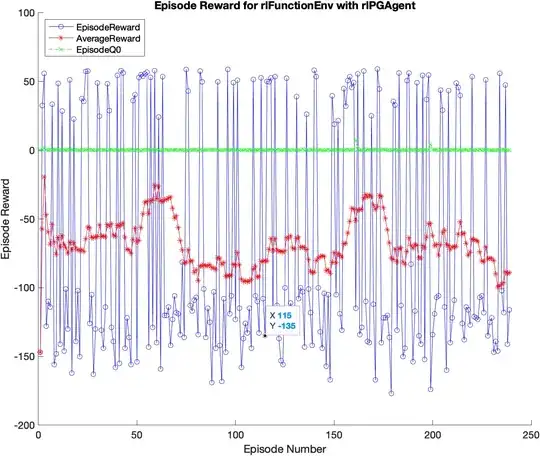
My current setup is using mostly default RL setups from MALTAB with learning rate of $10^{-4}$ and ADAM optimizer. The training is slow, and shows a lot of Reward oscillation between the two terminal states. MATLAB RL toolbox also outputs a $Q_0$ value which the state is:
Episode Q0 is the estimate of the discounted long-term reward at the start of each episode, given the initial observation of the environment. As training progresses, Episode Q0 should approach the true discounted long-term reward if the critic is well-designed,
Questions
- Is my training and episodes too random? i.e., time-series of different lengths and random initial sensor setup.
- Should I simplify my reward function to be just $T_2$?
- Why doesn't $Q_0$ change at all?