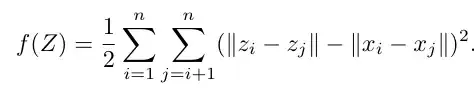Multiple-dimension scaling (MDS) objective for MDS and PCA

Question

The following is the MDS Objective.

Let's think of a senario where I apply MDS with/from the solution I obtained from PCA. Then I calculate the objective function on the initial PCA solution and MDS solution (after applying MDS on the former PCA solution). Then I would for sure assume that the objective function will decrease for the MDS solution compared with PCA solution. However, when I calculate the objective function respectively, MDS solution yields higher objective function value. Is this normal?

I am attaching my code below:

import os
import pickle
import gzip
import argparse
import time
import matplotlib.pyplot as plt
import numpy as np
from numpy.linalg import norm

from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
from sklearn.neural_network import MLPRegressor, MLPClassifier
from sklearn.preprocessing import LabelBinarizer
from sklearn import decomposition

from neural_net import NeuralNet, stochasticNeuralNet
from manifold import MDS, ISOMAP
import utils

def mds_objective(Z,X):
    sum = 0
    n,d = Z.shape
    for i in range(n):
        for j in range(i+1,n):
            sum += (norm(Z[i,:]-Z[j,:],2)-norm(X[i,:]-X[j,:],2))**2
    return 0.5*sum

dataset = load_dataset('animals.pkl')
X = dataset['X'].astype(float)
animals = dataset['animals']
n, d = X.shape
pca = decomposition.PCA(n_components = 5)
pca.fit(X)
Z = pca.transform(X)
plt.figure()
plt.scatter(Z[:, 0], Z[:, 1])
for i in range(n):
     plt.annotate(animals[i], (Z[i,0], Z[i,1]))
utils.savefig('PCA.png')

print(pca.explained_variance_ratio_)
print(mds_objective(Z,X))


dataset = load_dataset('animals.pkl')
X = dataset['X'].astype(float)
animals = dataset['animals']
n,d = X.shape

model = MDS(n_components=2)
Z = model.compress(X)

fig, ax = plt.subplots()
ax.scatter(Z[:,0], Z[:,1])
plt.ylabel('z2')
plt.xlabel('z1')
plt.title('MDS')
for i in range(n):
       ax.annotate(animals[i], (Z[i,0], Z[i,1]))
utils.savefig('MDS_animals.png')
print(mds_objective(Z,X))

It prints the following:

1673.1096816455256

1776.8183112784652