In regularzied cost function a L2 regularization cost has been added.
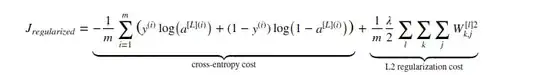
Here we have already calculated cross entropy cost w.r.t $A, W$.
As mentioned in the regularization notebook (see below) in order to do derivation of regularized $J$ (cost function), the changes only concern $dW^{[1]}$, $dW^{[2]}$ and $dW^{[3]}$. For each, you have to add the regularization term's gradient.(No impact on $dA^{[2]}$, $db^{[2]}$, $dA^{[1]}$ and $db^{[1]}$ ?)
But I am doing it using the chain rule then I am getting change in values for $dA^{[2]}$ , $dZ^{[2]}$, $dA^{[1]}$, $dW^{[1]}$ and $db^{[1]}$.
Please refer below how I calculated this ?

Can someone explain why I am getting different results?
What is the derivative of L2 reguarlization w.r.t $dA^{[2]}$ ? (in equation 1)
So my questions are
1) Derivative of L2 regularization cost w.r.t $dA^{[2]}$
2) How adding regularization term not affecting $dA^{[2]}$, $db^{[2]}$, $dA^{[1]}$ and $db^{[1]}$ (i.e. $dA$ and $db$) but changes $dW$'s ?
