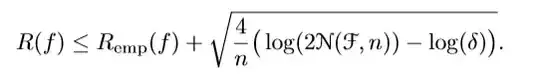Understanding relation between VC Symmetrization Lemma and Generalization Bounds

Question

I am new in the field of Machine Learning so I wanted to start of by reading more about mathematics and history behind it.

I am currently reading, in my opinion, a very good and descriptive paper on Statistical Learning Theory - "Statistical Learning Theory: Models, Concepts, and Results". In section 5.5 Generalization bounds, it states that:

It is sometimes useful to rewrite (17) "the other way round". That is, instead of fixing $\epsilon$ and then computing the probability that the empirical risk deviates from the true risk by more than $\epsilon$, we specify the probability with which we want the bound to hold, and then get a statement which tells us how close we can expect the risk to be to the empirical risk. This can be achieved by setting the right-hand side of (17) equal to some $\delta > 0$, and then solving for $\epsilon$. As a result, we get the statement that with a probability at least $1−\delta$, any function $f \in F$ satisfies

Equation (17) is VC Symmetrization lemma to which we applied union bound and then Chernoff bound:

What I fail to understand is the part where we are rewriting (17) "the other way around". I fail to grasp intuitive understanding of relation between (17) and (18), as well as understanding generalization bounds in general.

Could anyone help me with understanding these concepts or at least provide me with additional resources (papers, blog posts, etc.) that can help?

Answer 1

Let $\varepsilon$ in (17) is equal to $\sqrt{\frac{4}{n}\left(\log{(2\mathsf{N}(\mathcal{F},n))}-\log{\delta}\right)}$. We have:

$$ P\left(\sup_{f\in\mathcal{F}}|R(f)-R_{emp}(f)| > \sqrt{\frac{4}{n}\left(\log{(2\mathcal{N}(\mathcal{F},n))}-\log{\delta}\right)}\right) \leqslant 2\mathcal{N}(\mathcal{F},n) e^{\frac{-n}{4}\left(\frac{4}{n}\left(\log{(2\mathcal{N}(\mathcal{F},n))}-\log{\delta}\right)\right)} = 2\mathcal{N}(\mathcal{F},n) e^{\log{\delta} - \log{(2\mathcal{N}(\mathcal{F},n))}} $$

As we know that $e^{\log{n}} = n$ (suppose that base of $\log$ here is $e$), we can write:

$$ P\left(\sup_{f\in\mathcal{F}}|R(f)-R_{emp}(f)| > \sqrt{\frac{4}{n}\left(\log{(2\mathcal{N}(\mathcal{F},n))}-\log{\delta}\right)}\right) \leqslant 2\mathcal{N}(\mathcal{F},n) \left(\frac{\delta}{2\mathcal{N}(\mathcal{F},n)}\right) $$

Hence:

$$ P\left(\sup_{f\in\mathcal{F}}|R(f)-R_{emp}(f)| > \sqrt{\frac{4}{n}\left(\log{(2\mathcal{N}(\mathcal{F},n))}-\log{\delta}\right)}\right) \leqslant \delta $$ As we know that if we have $P(x > a) \leqslant c$, we can conlude that $P( x<a) \geqslant 1-c$, we will have:

$$ P\left(\sup_{f\in\mathcal{F}}|R(f)-R_{emp}(f)| < \sqrt{\frac{4}{n}\left(\log{(2\mathcal{N}(\mathcal{F},n))}-\log{\delta}\right)}\right) \geqslant 1- \delta $$

Now, as this inequality is true for supremum of set $\mathcal{F}$ and $R(f) -R_{emp}(f) \leqslant \varepsilon$ is subset of $|R(f) -R_{emp}(f)| \leqslant \varepsilon$ (in terms of probability state space), we can say the following inequality is correct for any function $f$ with at least probability of $1-\delta$: $$ R(f) \leqslant R_{emp}(f) + \sqrt{\frac{4}{n}\left(\log{(2\mathcal{N}(\mathcal{F},n))}-\log{\delta}\right)} $$