Loss function for choosing a subset of objects

Question

I'm trying to train a neural net to choose a subset from some list of objects. The input is a list of objects $(a,b,c,d,e,f)$ and for each list of objects the label is a list composed of 0/1 - 1 for every object that is in the subset, for example $(1,1,0,1,0,1)$ represents choosing $a,b,d,f$. I thought about using MSE loss to train the net but that seemed like a naive approach, is there some better loss function to use in this case?

Answer 1

The choice of the loss function depends primarily on the type of task you're tackling: classification or regression. Your problem is clearly a classification one since you have classes to which a given input can either belong or not. More specifically, what you're trying to do is multi-label classification, which is different from multi-class classification. The difference is important to stress out and it consists in the format of the target labels.

# Multi-class --> one-hot encoded labels, only 1 label is correct   
  
[1,0,0], [0,1,0], [0,0,1]

# Multi-label --> multiple labels can be correct
 
[1,0,0], [1,1,0], [1,1,1], [0,1,0], [0,1,1], [0,0,1]

MSE is used when continuous values are predicted for some given inputs, therefore it belongs to the loss functions suitable for regression and it should not be used for your problem.

Two loss functions that you could apply are Categorical Cross Entropy or Binary Cross Entropy. Despite being both based on cross-entropy, there is an important difference between them, consisting of the activation function they require.

Binary Cross Entropy

$$L(y, \hat{y})=-\frac{1}{N} \sum_{i=0}^{N}\left(y * \log \left(\hat{y}_{i}\right)+(1-y) * \log \left(1-\hat{y}_{i}\right)\right)$$

Despite the name that suggests this loss should be used only for binary classification, this is not strictly true and actually, this is the loss function that conceptually is best suited for multi-label tasks.

Let's start with the binary classification case. We have a model that returns a single output score, to which the sigmoid function is applied in order to constrain the value between 0 and 1. Since we have a single score, the resulting value can be interpreted as a probability of belonging to one of the two classes, and the probability of being to the other class can be computed as 1 - value.

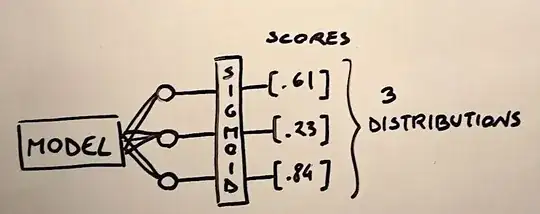
What if we have multiple output scores, for example, 3 nodes for 3 classes? In this case, we still could apply the sigmoid function, ending up with three scores between 0 and 1.

The important aspect to capture is that since the sigmoid treat each output node independently, the 3 scores would not sum up to 1, so they will represent 3 different probability distributions rather than a unique one. This means that each score after the sigmoid represents a distinct probability of belonging to that specific class. In the example above, for example, the prediction would be true for the two labels with a score higher than 0.5 and false for the remaining label. This also means that 3 different loss have to be computed, one for each possible output. In practice, what you'll be doing is to solve n binary classification problems where n is the number of possible labels.

Categorical Cross Entropy

$$L(y, \hat{y})=-\sum_{j=0}^{M} \sum_{i=0}^{N}\left(y_{i j} * \log \left(\hat{y}_{i j}\right)\right)$$

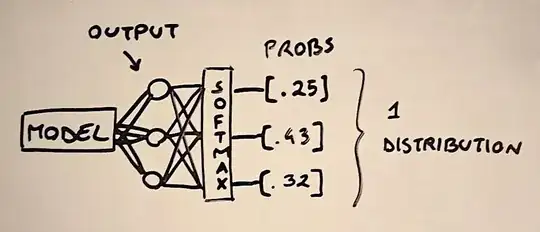
In categorical cross-entropy we apply the softmax function to the output scores of our model, to constrain them between 0 and 1 and to turn them into a probability distribution (they all sum to 1). The important thing to notice is that in this case, we end up with a unique distribution because, unlike the sigmoid function, the softmax consider all output scores together (they are summed in the denominator).

This implies that categorical cross-entropy is best suited for multi-class tasks, in which we end up with a single true prediction for each input instance. Nevertheless, this loss can also be applied also for multi-label tasks, as done in this paper. To do so, the authors turned each target vector into a uniform probability distribution, which means that the values of the true labels are not 1 but 1/k, with k being the total number of true labels.

# Example of target vector tuned into uniform probability distribution
[0, 1, 1] --> [0, .5, .5]  
[1, 1, 1] --> [.33, .33, .33]

Note also that in the above-mentioned paper the authors found that categorical cross-entropy outperformed binary cross-entropy, even this is not a result that holds in general.

Lastly, the are other loss that you could try which differ functions rather than cross-entropy, for example:

Hamming-Loss

It computes the fraction of wrong predicted labels

$$\frac{1}{|N| \cdot|L|} \sum_{i=1}^{|N|} \sum_{j=1}^{|L|} \operatorname{xor}\left(y_{i, j}, z_{i, j}\right)$$

Exact Match Ratio

Only predictions for which all target labels were correctly classified are considered correct.

$$ExactMatchRatio,\space M R=\frac{1}{n} \sum_{i=1}^{n} I\left(Y_{i}=Z_{i}\right)$$