What is the main contribution of the paper Disentangling by Factorising?

Question

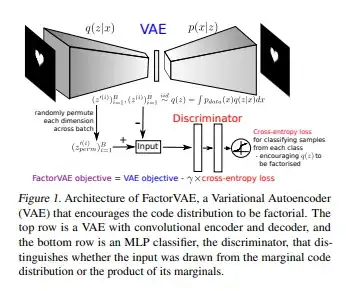
Considering the paper Disentangling by Factorising, in addition to introducing a new model for Disentangled Representation Learning, FactorVAE (see figure), what is the main theoretical contribution provided by the paper?

Answer 1

One of the core contributions presented in the paper consists of understanding at a deeper level the objective function used in Beta VAE and improving it

More specifically, the authors started from Beta VAE OF

$$\frac{1}{N} \sum_{i=1}^{N}\left[\mathbb{E}_{q\left(z | x^{(i)}\right)}\left[\log p\left(x^{(i)} | z\right)\right]-\beta K L\left(q\left(z | x^{(i)}\right) \| p(z)\right)\right]$$

which consists of the classical reconstruction loss and the regularization term which steers the Latent Code PDF towards a target PDF.

Developing the second term

$$\mathbb{E}_{p_{\text{data}}(x)}[K L(q(z | x) \| p(z))]=I(x ; z)+K L(q(z) \| p(z))$$

they observed there are 2 terms which push in different directions:

$I(x,z)$ is the mutual information between the input data and the code, and we do not want to penalize this as in fact we want this to be as high as possible, so that the decode contains as much information as possible about the input $KL(q(z) || p(z))$ is the KL divergence term which if penalized pushes the latent code PDF $q(z)$ towards the prior $p(z)$ which we choose as factorized So penalizing the second term in Beta VAE OF means also penalizing the mutual information hence ultimately loosing reconstruction capability

The authors then propose a new OF which fixes this

$$\frac{1}{N} \sum_{i=1}^{N}\left[\mathbb{E}_{q\left(z | x^{(i)}\right)}\left[\log p\left(x^{(i)} | z\right)\right]-K L\left(q\left(z | x^{(i)}\right)|| p(z)\right)\right] -\gamma K L(q(z) \| \bar{q}(z))$$

In the rest of the paper they run experiments and show they have improved the disentanglement of the representation (according to the new metric they propose in the paper) while preserving reconstruction hence improving the reconstruction vs disentanglement tradeoff with respect to the Beta VAE paper