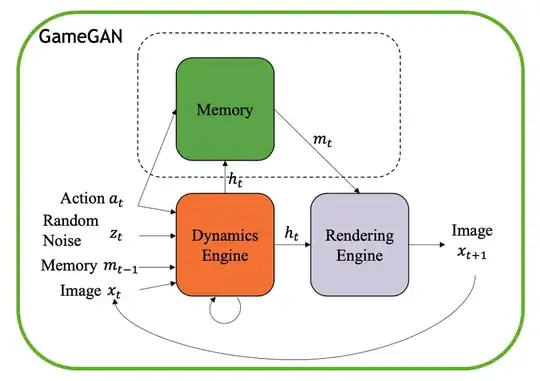
Seung et.al recently published GameGAN paper, GameGAN learned and stored the whole Pacman game and was able to reproduce it without a game engine. The uniqueness of GameGAN is that it had added memory to its discriminator/generator which helped it to store the game states.
In Bayesian interpretation, a supervised learning system learns by optimizing weights which maximizes a likelihood function.
$$\hat{\boldsymbol{\theta}} = \mathop{\mathrm{argmax}} _ {\boldsymbol{\theta}} P(X \mid \boldsymbol{\theta})$$
Will adding memory which can store prior information makes GameGAN a Bayesian learning system?
Can GameGAN or similar neural network with memory can be considered as a bayesian learning system. If yes, then which of these two equations(or something other) correctly explains this system (considering prior as memory)?
- $$\mathop{\mathrm{argmax}} \frac{P(X \mid \boldsymbol{\theta})P(\boldsymbol{\theta})}{P(X)}$$
or
- $$\mathop{\mathrm{argmax}} \frac{P(X_t \mid \boldsymbol{X^{t+1}})P(\boldsymbol{X^{t+1}})}{P(X_t)}$$
PS: I understand GAN's are unsupervised learning systems, but we can assume discriminator and generator models separately trying to find weights that maximize their individual likelihood function.