What is the definition of the "cost" function in the SVM's objective function?

Question

In a course that I am attending, the cost function of a support vector machine is given by

$$J(\theta)=\sum_{i=1}^{m} y^{(i)} \operatorname{cost}_{1}\left(\theta^{T} x^{(i)}\right)+\left(1-y^{(i)}\right) \operatorname{cost}_{0}\left(\theta^{T} x^{(i)}\right)+\frac{\lambda}{2} \sum_{j=1}^{n} \Theta_{j}^{2}$$

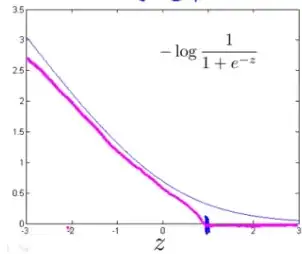
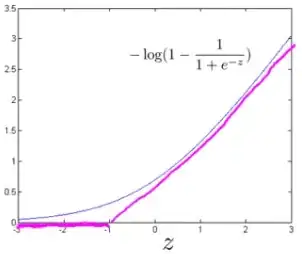
where $\operatorname{cost}_{1}$ and $\operatorname{cost}_{0}$ look like this (in Magenta):

What are the values of the functions $\operatorname{cost}_{1}$ and $\operatorname{cost}_{0}$?

For example, if using logistic regression the values of $\operatorname{cost}_{1}$ and $\operatorname{cost}_{0}$ would be $-\log* \operatorname{sigmoid}(-z)$ and $-\log*(1-\operatorname{sigmoid}(-z))$.

Answer 1

That is the hinge loss, a type of loss most notably used for SVM classification. The hinge loss is typically defined as:

$$ \ell(y)=\max (0,1-t \cdot y), $$

which, in your use case, is something like this:

$$ \operatorname{cost}\left(h_{\theta}(x), y\right)=\left\{\begin{array}{ll} \max \left(0,1-\theta^{T} x\right) & \text { if } y=1 \\ \max \left(0,1+\theta^{T} x\right) & \text { if } y=0 \end{array}\right. $$

Check this article on it.