3

In this article I am reading:

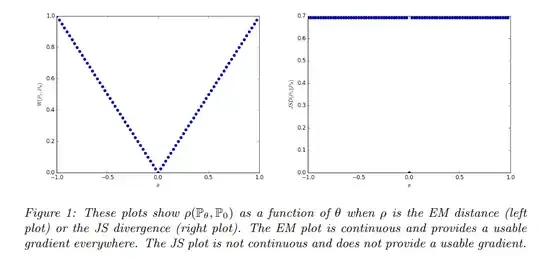
$D_{KL}$ gives us inifity when two distributions are disjoint. The value of $D_{JS}$ has sudden jump, not differentiable at $\theta=0$. Only Wasserstein metric provides a smooth measure, which is super helpful for a stable learning process using gradient descents.

Why is this important for a stable learning process? I have also the feeling this is also the reason for mode collapse in GANs, but I am not sure.

The Wasserstein GAN paper also talks about it obviously, but I think I am missing a point. Does it say JS does not provide a usable gradient? What exactly does that mean?

nbro
  • 39,006
  • 12
  • 98
  • 176
craft
  • 131
  • 1

1 Answers1

2

I don't have a definite answer, but only a suspicion/idea:

Looking at Figure 1 from the WGAN paper, we clear see that the JS divergence on the right is not continuous at $0$, hence not differentiable at $0$. However, the EM plot on the left is continuous also at $0$. You could now argue that we have a kink there, so it should not be differentiable there either, but they might have a different notion of differentiability, I am honestly not sure about it right now. enter image description here

Anonymous5638
  • 171
  • 5
  • There is a fairly straightforward way of doing optimization of piecewise linear functions that would deal fine with the left hand side, the non-differentiability at the 'kink' is not an issue, see e.g. [here](http://www.seas.ucla.edu/~vandenbe/ee236a/lectures/pwl.pdf) – Stiofán Fordham Jan 25 '21 at 21:34