4

I have been working on some RL project, where the policy is controlling the robot using its joint angles.Throughout the project I have noticed some phenomenon, which caught my attention. I have decided to create a very simplified script to investigate the problem. There it goes:

The environment

There is a robot, with two rotational joints, so 2 degrees of freedom. This means its continuous action space (joint rotation angle) has a dimensionality of 2. Let's denote this action vector by a. I vary the maximum joint rotation angle per step from 11 to 1 degrees and make sure that the environment is allowed to do a reasonable amounts of steps before the episode is forced to terminate on time-out.

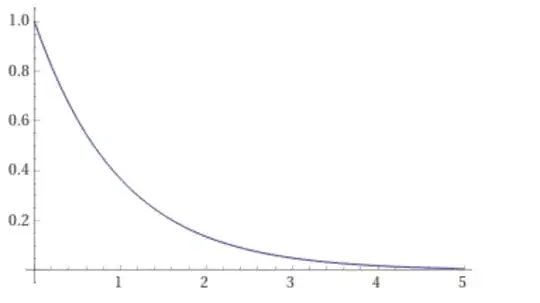
Our goal is to move the robot by getting its current joint configuration c closer to the goal joint angle configuration g (also two dimensional input vector). Hence, the reward I have chosen is e^(-L2_distance(c, g)).

The smaller the L2_distance, the exponentially higher the reward, so I am sure that the robot is properly incentivised to reach the goal quickly.

Reward function (y-axis: reward, x-axis: L2 distance):

Reward function (y-axis: reward, x-axis: L2 distance)

So the pseudocode for every step goes like:

  • move the joints by predicted joint angle delta

  • collect the reward

  • if time-out or joint deviates too much into some unrealistic configuration: terminate.

Very simple environment, not to have too many moving parts in our problem.

RL algorithm

I use Catalyst framework to train my agent in the actor-critic setting using TD3 algorithm. By using a tested framework, which I am quite familiar with, I am quite sure that there are no implementational bugs.

The policy is goal-driven so the actor consumes the concatenated current and goal joint configuration a= policy([c,g])

The big question

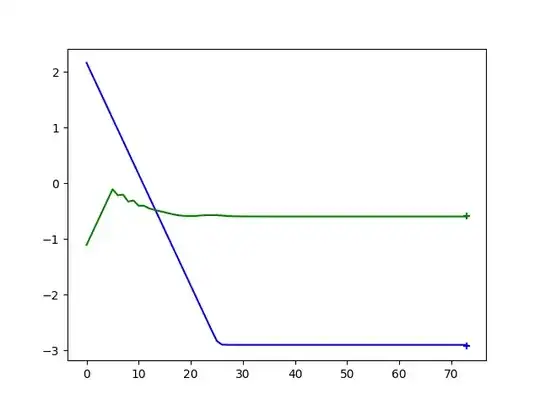
When the robot has only two degrees of freedom, the training quickly converges and the robots learns to solve the task with high accuracy (final L2 distance smaller than 0.01).

Performance of the converged 2D agent. y-axis: joint angle value, x-axis: no of episodes. Crosses denote the desired goal state of the robot.:

Performance of the converged 2D agent. y-axis: joint angle value, x-axis: no of episodes. Crosses denote the desired goal state of the robot.

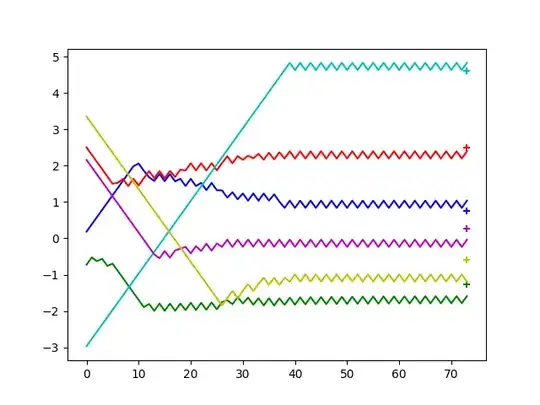
However, if the problem gets more complicated - I increase the joint dimensions to 4D or 6D, the robot initially learns to approach the target, but it never "fine-tunes" its movement. Some joints tend to oscillate around the end-point, some of them tend to overshoot.

I have been experimenting with different ideas: making the network wider and deeper, changing the action step. I have not tried optimizer scheduling yet. No matter how many samples the agent receives or how long it trains, it never learns to approach targets with required degree of accuracy (L2_distance smaller than 0.05).

Performance of the converged 4D agent. y-axis: joint angle value, x-axis: no of episodes. Crosses denote the desired goal state of the robot.:

Performance of the converged 4D agent. y-axis: joint angle value, x-axis: no of episodes. Crosses denote the desired goal state of the robot.

Training curve for 2D agent (red) and 4D agent (orange). 2D agent quickly minimises the L2 distance to something smaller than 0.05, while the 4D agent struggles to go below 0.1.:

Training curve for 2D agent (red) and 4D agent (orange). 2D agent quickly minimises the L2 distance to something smaller than 0.05, while the 4D agent struggles to go below 0.1.

Literature research

I have looked into papers which describe motion planning in joint space using TD3 algorithm.

There are not many differences from my approach: Link 1 Link 2

Their problem is much more difficult because the policy needs to also learn the model of the obstacles in joint space, not only the notion of the goal. The only thing which is special about them is that they use quite wide and shallow networks. But this is the only peculiar thing. I am really interested, what do you guys would advise me to do, so that the robot can reach high accuracy in higher joint configuration dimensions? What am I missing here?!

Thanks for any help in that matter!

Shayan Shafiq
  • 350
  • 1
  • 4
  • 12
dtransposed
  • 41
  • 1
  • 1
    Are all episodes the same length regardless of getting close to the goal state? E.g. they are all 75 time steps long, and a perfect, lucky agent could score +75 total reward if it started in the goal state and did not move? – Neil Slater Oct 10 '20 at 13:58
  • Yes, the setup is exactly as you describe it. This perfect, lucky agent could observe that situation in theory. But the probability of such an episode is so low that I do not consider this harmful by any means. Could you elaborate on your comment? Do you think there might be a problem with the setup? – dtransposed Oct 10 '20 at 16:56
  • I don't think the possible +75 episode by accident is a problem. I just wanted to confirm that the episode does not end due to getting the correct value, and that is the extreme case. I originally wrote an answer assuming that reaching the goal would terminate an episode - that answer is not correct for your setup, so I deleted it – Neil Slater Oct 10 '20 at 16:58
  • Well, now when you explained your point of view: I have currently this "termination on success" condition implemented for 4D robot. But to be honest, IMO, it does not change anything, because the required L2 distance is so low, that the "success" condition never gets triggered in the 4D case. EDIT: So to be clear, agent always reaches 75 steps before termination and never reaches the success state. It only collects the reward based on the exponential of l2 distance. – dtransposed Oct 10 '20 at 17:02
  • "termination on success" will be a major problem for you, and if you decide you want to keep that rule, you will need to change your reward function. When you say it "never reaches the success state" is that strictly true during all training episodes, or are there a small fraction of times when it happens (perhaps apparently by accident and early on during training)? – Neil Slater Oct 10 '20 at 18:25
  • 1. Yes, its strictly true, I keep logging that. 2. Why termination on success is a problem? I don't see how this could harm the training. – dtransposed Oct 10 '20 at 19:23
  • Termination on success is a problem in your case - with your reward signal - because it zeroes out the remaining rewards. In your reward scheme, the agent is incentivised to get close to the goal but not too close otherwise it would lose rewards from remaining time steps. There are a few ways to fix this - for instance you could end with +75 reward, guaranteed to be better than anything the agent could get by waiting. However, you are not hitting that problem yet for some other reason that I cannot quite see. – Neil Slater Oct 10 '20 at 21:23
  • I understand your point, I see how this can be a problem in theory, but it does not explain why 2D agent "gets it right" and 4D does not. – dtransposed Oct 11 '20 at 10:13

0 Answers0