What is the impact of scaling the KL divergence and reconstruction loss in the VAE objective function?

Question

Variational autoencoders have two components in their loss function. The first component is the reconstruction loss, which for image data, is the pixel-wise difference between the input image and output image. The second component is the Kullback–Leibler divergence which is introduced in order to make image encodings in the latent space more 'smooth'. Here is the loss function:

\begin{align} \text { loss } &= \|x-\hat{x}\|^{2}+\operatorname{KL}\left[N\left(\mu_{x}, \sigma_{x}\right), \mathrm{N}(0,1)\right] \\ &= \|x-\mathrm{d}(z)\|^{2}+\operatorname{KL}\left[N\left(\mu_{x^{\prime}} \sigma_{x}\right), \mathrm{N}(0,1)\right] \end{align}

I am running some experiments on a dataset of famous artworks using Variational Autoencoders. My question concerns scaling the two components of the loss function in order to manipulate the training procedure to achieve better results.

I present two scenarios. The first scenario does not scale the loss components.

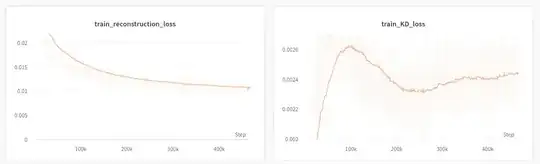
Here you can see the two components of the loss function. Observe that the order of magnitude of the Kullback–Leibler divergence is significantly smaller than that of the reconstruction loss. Also observe that 'my famous' paintings have become unrecognisable. The image shows the reconstructions of the input data.

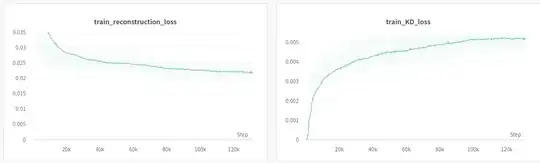
In the second scenario I have scaled the KL term with 0.1. Now we can see that the reconstructions are looking much better.

Question

1. Is it mathematically sound to train the network by scaling the components of the loss function? Or am I effectively excluding the KL term in the optimisation?

2. How to understand this in terms of gradient descent?

3. Is it fair to say that we are telling the model "we care more about the image reconstructions than 'smoothing' the latent space"?

I am confident that my network design (convolutional layers, latent vector size) have the capacity to learn parameters to create proper reconstructions as a Convolutional Autoencoder with the same parameters is able to reconstruct perfectly.

Here is a similar question.

Image Reference: https://towardsdatascience.com/understanding-variational-autoencoders-vaes-f70510919f73

Answer 1

Ans 1.

The motive of Variational Inference(on which VAE is based), is to decrease $KL(q(z|x)||p(z))$, where p(z) is our chosen distribution of the hidden variable z. After doing some math, we can write this expression as-

$ KL(q||x) = log(p(x)) - \Sigma_z q(z)log(\frac{p(x,z)}{q(z)}) $

For a given x, the first term of RHS is constant. So we maximise the second term so that the KL divergence goes to zero.

We can write the second term as

$E_{q(z)}[log(p(x|z)] - KL(q(z|x)||p(z))$

(try writing p(x,z) as $\frac{p(x|z)}{p(z)}$ and then expand. Here, p(z) is the distribution of our choice, i.e. a Gaussian distribution). We argue that the process from z to x is deterministic and z is gaussian. So, the first term could be replaced by $exp(log(-||x-\hat{x}||^2))$(we replaced z by $\hat{x}$ because it's deterministic- this is now the exact proof). So we have-

$ maximize(-||x-\hat(x)||-KL(q(z|x)||p(z))) $

and we get our loss function.

We also know that variational autoencoders almost never find the optimal solution, so I am not sure how would playing around with the weights affect it(Nor do I know if it makes sense mathematically).

Ans 2.

We can say that the KL divergence has a regularising effect.

This page has some nice experiments which will help you understand what happens to the latent space when you decrease the KL divergence part.

Ans 3.

Yes, you can say that. You are fixing the dimensions, but are lenient on the distribution. In fact, you are approaching autoencoders by doing this.

Separate-

I want to point you towards this article. It explains why we choose to minimise $KL(q(z|x)||p(z))$ instead of $KL(p(z)||q(z|x))$ (the latter is intractable) and what would happen if we choose less independent variables for our estimator q(z).

Also, have you tried increasing the dimensions of the latent space? It can also have a 'de-regularizing' effect. It seems that the model is underfitting the data- the reconstruction loss is high with the normal loss, compared to when you decrease the regularizing term.

Hope it helps.