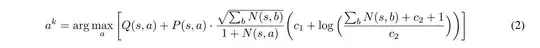I had the same question and found this page, then I also started to look at the pseudo-code of Supplementary Materials. The code of the computation of the UCB score is as followed:
# The score for a node is based on its value, plus an exploration bonus based on
# the prior.
def ucb_score(config: AlphaZeroConfig, parent: Node, child: Node):
pb_c = math.log((parent.visit_count + config.pb_c_base + 1) /
config.pb_c_base) + config.pb_c_init
pb_c *= math.sqrt(parent.visit_count) / (child.visit_count + 1)
prior_score = pb_c * child.prior
value_score = child.value()
return prior_score + value_score
I was very confused since it is different from the formula described in the paper, until I found the UCB formula in the paper of MuZero:
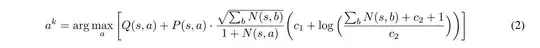
It is clear that the pseudocode of AlphaZero mistook the UCB formula of MuZero.
As for the original question, the sum of all the visit count numbers of the childen is implemented as the visit count of the parent node, which is at least 1, since it is visited as it is expanded (evaluated), as you can see in the code of the search:
# Core Monte Carlo Tree Search algorithm.
# To decide on an action, we run N simulations, always starting at the root of
# the search tree and traversing the tree according to the UCB formula until we
# reach a leaf node.
def run_mcts(config: AlphaZeroConfig, game: Game, network: Network):
root = Node(0)
evaluate(root, game, network)
add_exploration_noise(config, root)
for _ in range(config.num_simulations):
node = root
scratch_game = game.clone()
search_path = [node]
while node.expanded():
action, node = select_child(config, node)
scratch_game.apply(action)
search_path.append(node)
value = evaluate(node, scratch_game, network)
backpropagate(search_path, value, scratch_game.to_play())
return select_action(config, game, root), root