1

I'm not very knowledgeable in this field but I'm wondering if any research or information already exists for the following situation:

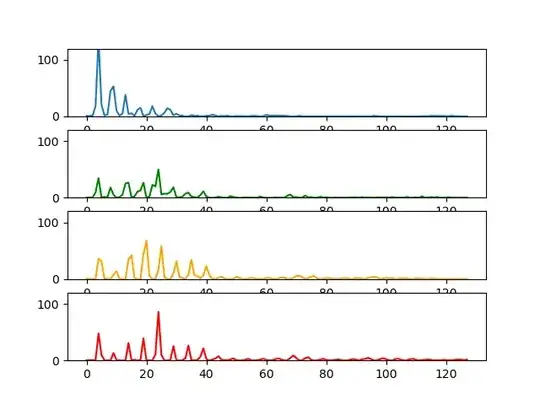
I have some data that may or may not look similar to each other. Each represents a node that represents a vector of size 128.

similar vectors

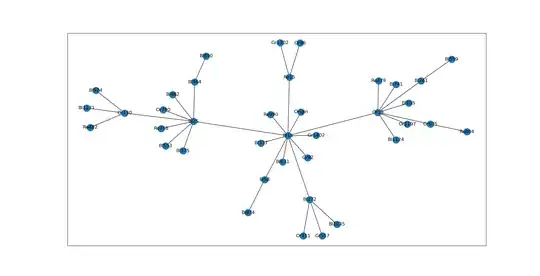
And they are inserted into a tree graph according to similarity.

better graph

and a new node is created with an edge connecting the most similar vertex node found in the entire tree graph.

Except I'm wasting a lot of time searching through the entire graph to insert each new node when I could narrow down my search according to previous information. Imagine a trunk node saying "Oh, I saw a node like you before, it went down this branch. And don't bother going down that other branch." I could reduce the cost of searching the entire tree structure if there was a clever way to remember if a similar node went down a certain path.

I've thought about some ways to use caching or creating a look-up table but these are very memory intensive methods and will become slower the longer the program runs on. I have some other ideas I am playing around with but I was hoping someone could point me in the right direction before I started trying out weird ideas.

Edit: added a better (more realistic) graph picture

JungleBird
  • 11
  • 2
  • might be late, but if your similarity metric abide the triangle inequality $d(a,c) \leq d(a,b) + d(b,c)$, you can use M-Tree (metric tree) to store/retrieve the node more efficiently. You can also query K-closest node by using M-Tree. – Sanyou Oct 05 '21 at 05:40
  • 1
    Thank you for answering! That's a great idea to explore, as I haven't seen a good solution to tackle this problem yet – JungleBird Oct 06 '21 at 22:58

1 Answers1

0

It sounds like you may be looking for the A* search algorithm. It is a search algorithm, like DFS and BFS, but it will explore only the most promising branches based on a heuristic function you supply. The difficult part of implementing this is deciding on a low-cost, admissible heuristic.

Excited to reflect nbro's suggestion from comments.

Alina Barnett
  • 56
  • 3
  • 1
    A* does not really prune branches, but it explores branches according to the admissible heuristic, so, more intuitively, we could say that it explores branches based on how promising they are, but it doesn't really discard any branch. I'm not sure if A* is really the solution the problem. – nbro Jan 04 '21 at 21:57
  • 1
    I would say that within the search space branches are "pruned" if they are never explored. Is there other terminology for that you would look for? – Alina Barnett Jan 05 '21 at 16:17
  • The reason why I think "prune" may not be the most appropriate term here is that, if there's no goal and the graph is finite, for instance, A* should explore all nodes, so, in that case, it doesn't prune anything. However, you're right that it may not visit certain parts of the search space if all paths that lead to the goal from a start node have already been explored, so, in those cases, we can think of certain parts of the search space being pruned. So, I was a bit imprecise in my previous comment, so your description was right (but not applicable in all cases). – nbro Jan 05 '21 at 16:22
  • In any case, I'm still not sure whether A* is the right tool to solve OP's problem. Maybe you should try to explain more in detail how A* should be applied in the OP's case. – nbro Jan 05 '21 at 16:27
  • 1
    Thank you guys for answering my question! I didn't know that kind of search algorithm was called the A* search algorithm. But nbro has a point since it seems like the A* algorithm requires a destination to work towards. This problem is a real head-scratcher because the data isn't discrete; it's like drawing lines in the sand to mark how far the waves reach into the beach. Using a heuristic has it's merits but it breaks down when that heuristic comes down to a razor's margin at a fork in the road. – JungleBird Jan 06 '21 at 05:31
  • I also edited my post to include a better picture of a graph I'd be dealing with. Each branch represents a cluster/sub-cluster. And it would reduce my search time exponentially if I could just "prune" the first few major branches and contain my DFS/BFS in a sub-cluster. The best way to do that would be keep some memory about where previous nodes ended up. At first the associations would be weak but grow stronger with more nodes being placed, and stronger associations would translate to greater confidence in which path a node should take. – JungleBird Jan 06 '21 at 05:57