There are proofs for the universal approximation theorem with just 1 hidden layer.
The proof goes like this:
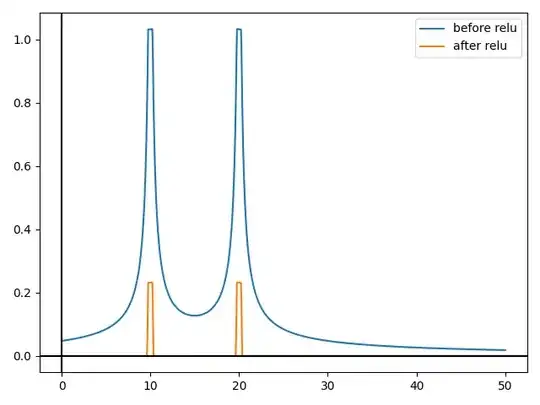
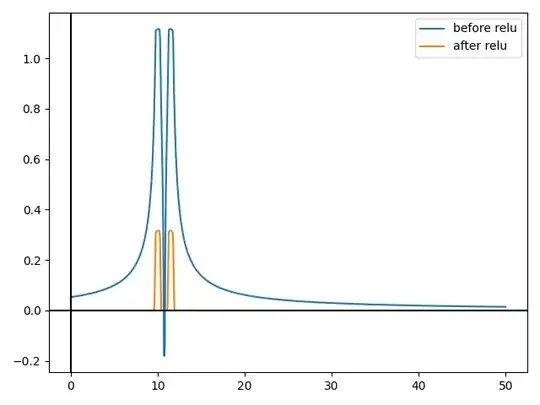
Create a "bump" function using 2 neurons.
Create (infinitely) many of these step functions with different angles in order to create a tower-like shape.
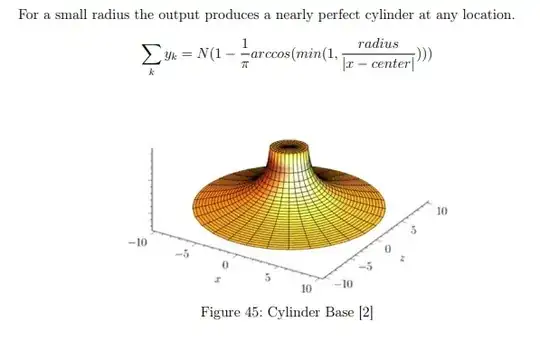
Decrease the step/radius to a very small value in order to approximate a cylinder. This is what I'm not convinced of
Using these cylinders one can approximate any shape. (At this point it's basically just a packing problem like this.
In this video, minute 42, the lecturer says
In the limit that's going to be a perfect cylinder. If the cylinder is small enough. It's gonna be a perfect cylinder. Right ? I have control over the radius.
Here are the slides.
Here is a pdf version from another university, so you do not have to watch the video.
Why am I not convinced?
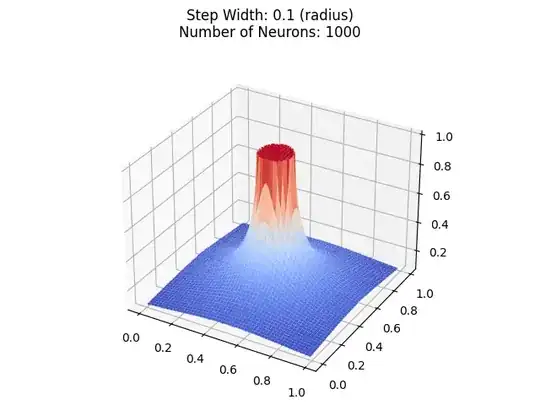
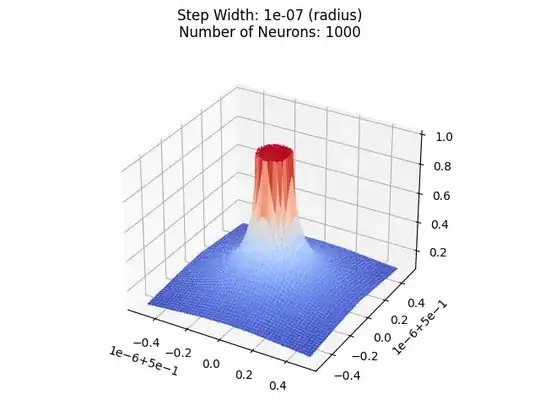
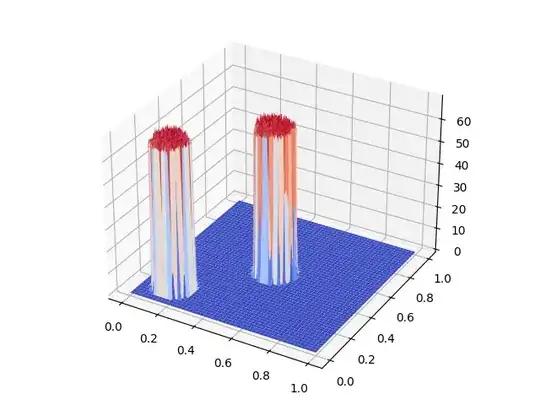
I created a program to plot this, and even if I decrease the radius by orders of magnitude it still has the same shape.
Let's start with a simple tower of radius 0.1:
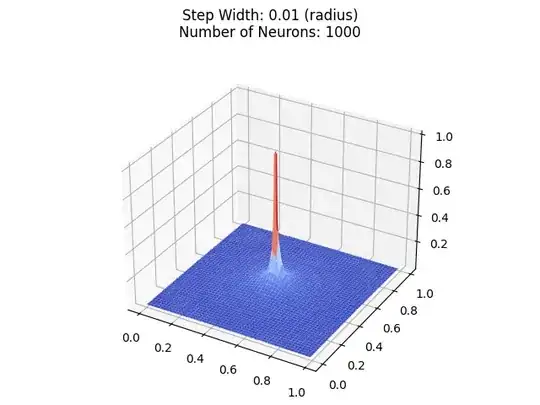
Now let's decrease the radius to 0.01:
Now, you might think that it gets close to a cylinder, but it just looks like it is approximating a perfect cylinder, because of the zoomed out effect.
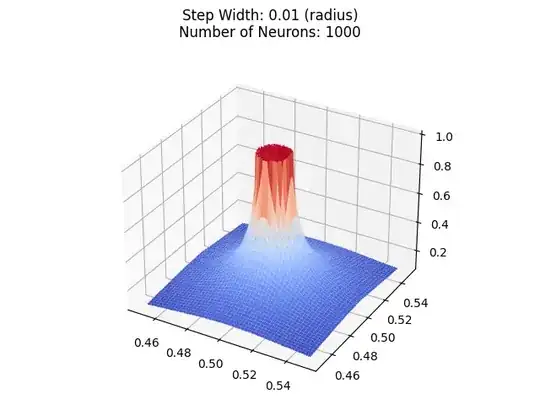
Let's zoom in:
Let's decrease the radius to 0.0000001.
Still not a perfect cylinder. In fact, the "quality" of the cylinder is the same.
Python code to reproduce (requires NumPy and matplotlib): https://pastebin.com/CMXFXvNj.
So my questions are:
Q1 Is it true that we can get a perfect cylinder solely by decreasing the radius of the tower to 0 ?
Q2 If this true, why is there no difference when I plot it with different radii(0.1, vs 1e-7) ?
Both towers have the same shape
Clarification: What do I mean with: same shape ? Let's say we calculate the volume of an actual cylinder(Vc) with the same raius and height as our tower and divide it by the volume of the tower(Vt) .
Vc = Volume Cylinder
Vt = Volume Tower
ratio(r) = Vc/Vt
What this documents/lectures claim that is the ratio of these 2 volumes depends on the radius but in my view it's just constant.
So what they are saying is that: lim r -> 0 for ratio(r) = 1 But my experiments show that: lim r -> 0 for ratio(r) = const and don't depend on the radius at all.
Q3 Preface
An objection i got multiple times once from Dutta and once from D.W is that just decreasing the radious and plotting it isn't mathematical rigorous.
So let's assume in the limit of r=0 it's really a perfect cylinder.
One possible explanation for this would be that the limit is a special case and one can't approximate towards it
But if that is true this would imply that there is no use for it since it's impossible to have a radius of exactly zero. It would only be useful if we could get gradually closer to a perfect cylinder by decreasing the radius.
Q3 So why should we even care about this then ?
Further Clarifications
The original universal approximation theorem proof for single hidden layer neural networks was done by G. Cybenko. Then I think people tried to make some visual explations for it. I am NOT questioning the paper ! But i am questioning the visual explanation given in the linked lecutre/pdf (made by other people)