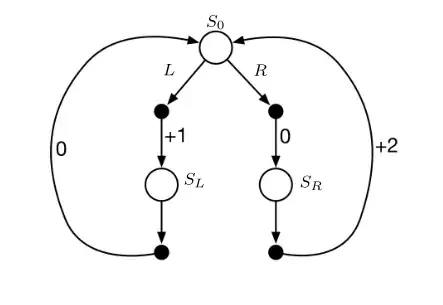
I am reading this paper Anxiety, Avoidance and Sequential Evaluation and is confused about the implementation of a specific lab study. Namely, the authors model what is called the Balloon task using a simple MDP for which the description is below:
My confusion is the following sentence:
...The probability of this bad transition was modeled using normal density function, with parameters $N(16, 0.5)$
But the fact that this is a continuous, normal distribution makes me stumped. In MDP's, usually there is a nice, discrete transition matrix and so there is no ambiguity as to how to implement it. For instance, if they said the transition to a bad state is modeled by a Bernoulli random variable with parameter $p,$ then it is clear how to implement it. I would do something like:
def step(curr_state, curr_action):
if uniform random variable(0,1) < p:
next_state = bad state
But they are using a normal random variable for this "bad" transition, so how do I implement this?