I know I can make a VAE do generation with a mean of 0 and std-dev of 1. I tested it with the following loss function:
def loss(self, data, reconst, mu, sig):
rl = self.reconLoss(reconst, data)
#dl = self.divergenceLoss(mu, sig)
std = torch.exp(0.5 * sig)
compMeans = torch.full(std.size(), 0.0)
compStd = torch.full(std.size(), 1.0)
dl = kld(mu, std, compMeans, compStd)
totalLoss = self.rw * rl + self.dw * dl
return (totalLoss, rl, dl)
def kld(mu1, std1, mu2, std2):
p = torch.distributions.Normal(mu1, std1)
q = torch.distributions.Normal(mu2, std2)
return torch.distributions.kl_divergence(p, q).mean()
In this case, mu and sig are from the latent vector, and reconLoss is MSE. This works well, and I am able to generate MNIST digits by feeding in noise from a standard normal distribution.
However, I'd now like to concentrate the distribution at a normal distribution with std-dev of 1 and mean of 10. I tried changing it like this:
compMeans = torch.full(std.size(), 10.0)
I did the same change in reparameterization and generation functions. But what worked for the standard normal distribution is not working for the mean = 10 normal one. Reconstruction still works fine but generation does not, only producing strange shapes. Oddly, the divergence loss is actually going down too, and reaching a similar level to what it reached with standard normal.
Does anyone know why this isn't working? Is there something about KL that does not work with non-standard distributions?
Other things I've tried:
- Generating from 0,1 after training on 10,1: failed
- Generating on -10,1 after training on 10,1: failed
- Custom version of KL divergence: worked on 0,1. failed on 10,1
- Using sigma directly instead of std = torch.exp(0.5 * sig): failed
Edit 1:
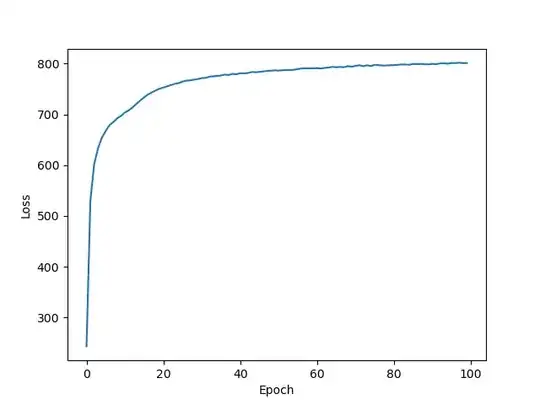
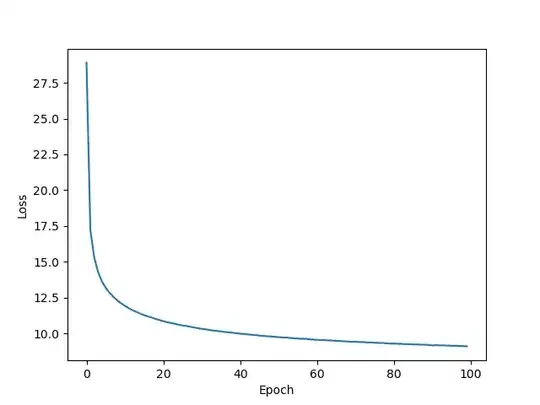
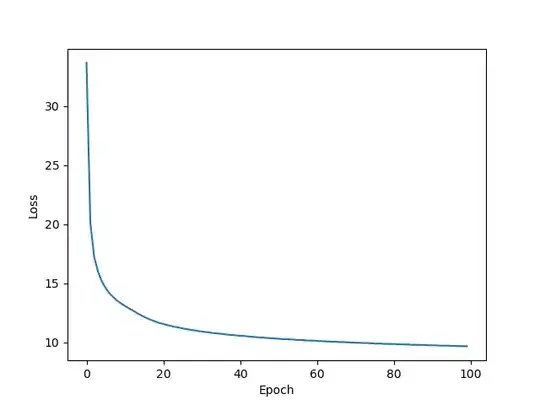
Below are my loss plots with 0,1 distribution.
Reconstruction:
Reconstruction samples (left is input, right is output):
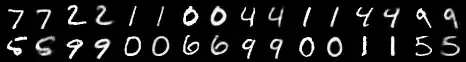
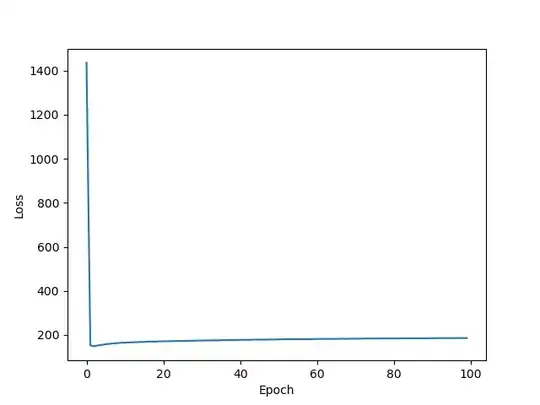
And here are the plots for 10,1 normal distribution.
Note: when I ran it this time, it actually seemed to learn the generation a bit, though it's still printing mostly 8's or things that are nearly an 8 by structure. This is not the case for the standard normal distribution. The only difference from last run is the random seed.
Sampled latent:
tensor([[ 9.6411, 9.9796, 9.9829, 10.0024, 9.6115, 9.9056, 9.9095, 10.0684,
10.0435, 9.9308],
[ 9.8364, 10.0890, 9.8836, 10.0544, 9.4017, 10.0457, 10.0134, 9.9539,
10.0986, 10.0434],
[ 9.9301, 9.9534, 10.0042, 10.1110, 9.8654, 9.4630, 10.0256, 9.9237,
9.8614, 9.7408],
[ 9.3332, 10.1289, 10.0212, 9.7660, 9.7731, 9.9771, 9.8550, 10.0152,
9.9879, 10.1816],
[10.0605, 9.8872, 10.0057, 9.6858, 9.9998, 9.4429, 9.8378, 10.0389,
9.9264, 9.8789],
[10.0931, 9.9347, 10.0870, 9.9941, 10.0001, 10.1102, 9.8260, 10.1521,
9.9961, 10.0989],
[ 9.5413, 9.8965, 9.2484, 9.7604, 9.9095, 9.8409, 9.3402, 9.8552,
9.7309, 9.7300],
[10.0113, 9.5318, 9.9867, 9.6139, 9.9422, 10.1269, 9.9375, 9.9242,
9.9532, 9.9053],
[ 9.8866, 10.1696, 9.9437, 10.0858, 9.5781, 10.1011, 9.8957, 9.9684,
9.9904, 9.9017],
[ 9.6977, 10.0545, 10.0383, 9.9647, 9.9738, 9.9795, 9.9165, 10.0705,
9.9072, 9.9659],
[ 9.6819, 10.0224, 10.0547, 9.9457, 9.9592, 9.9380, 9.8731, 10.0825,
9.8949, 10.0187],
[ 9.6339, 9.9985, 9.7757, 9.4039, 9.7309, 9.8588, 9.7938, 9.8712,
9.9763, 10.0186],
[ 9.7688, 10.0575, 10.0515, 10.0153, 9.9782, 10.0115, 9.9269, 10.1228,
9.9738, 10.0615],
[ 9.8575, 9.8241, 9.9603, 10.0220, 9.9342, 9.9557, 10.1162, 10.0428,
10.1363, 10.3070],
[ 9.6856, 9.7924, 9.9174, 9.5064, 9.8072, 9.7176, 9.7449, 9.7004,
9.8268, 9.9878],
[ 9.8630, 10.0470, 10.0227, 9.7871, 10.0410, 9.9470, 10.0638, 10.1259,
10.1669, 10.1097]])
Note, this does seem to be in the right distribution.
Just in case, here's my reparameterization method too. Currently with 10,1 distribution:
def reparamaterize(self, mu, sig):
std = torch.exp(0.5 * sig)
epsMeans = torch.full(std.size(), 10.0)
epsStd = torch.full(std.size(), 1.0)
eps = torch.normal(epsMeans, epsStd)
return eps * std + mu