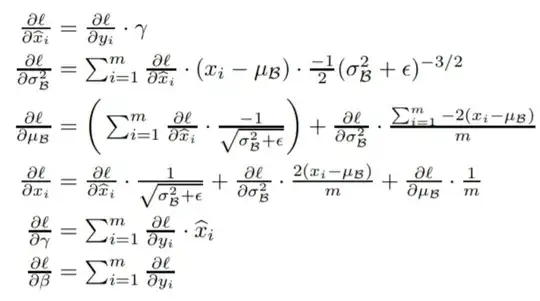From the original paper and this post we have that batch normalization backpropagation can be formulated as
I'm interested in the derivative of the previous layer outputs $x_i=\sigma(w X_i+b)$ with respect to $b$, where $\{X_i\in\mathbb{R}, i=1,\dots,m\}$ is a network input batch and $\sigma$ is some activation function with weight $w$ and bias $b$.
I'm using Adam optimizer so I average the gradients over the batch to get the gradient $\theta=\frac{1}{m}\sum_{i=1}^m\frac{\partial l}{\partial x_i}\frac{\partial x_i}{\partial b}$. Further, $\frac{\partial x_i}{\partial b}=\frac{\partial}{\partial b}\sigma(wX_i+b)=\sigma'(wX_i+b)$.
I am using ReLu activation function and all my inputs are positive, i.e. $X_i>0 \ \forall i$, as well as $w>0$ and $b=0$. That is, I get $\frac{\partial x_i}{\partial b} = 1\ \forall i$. That means that my gradient $\theta=\frac{1}{m}\sum_{i=1}^m\frac{\partial l}{\partial x_i}$ is just the average over all derivatives of the loss function with respect to $x_i$. But summing all the $\frac{\partial l}{\partial x_i}$ up is zero, which can be seen from the derivations of $\frac{\partial l}{\partial x_i}$ and $\frac{\partial l}{\partial \mu_B}$.
This means that my bias change would always be zero, which makes no sense to me. Also i created a neural network in Keras just for validation and all my gradients match except the bias gradients, which are not always zero in Keras.
Does one of you know where my mistake is in the derivation? Thanks for the help.