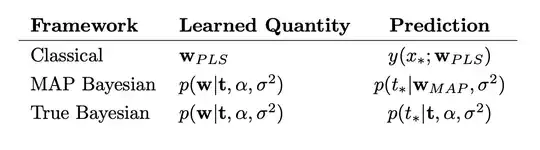Does the Bayesian MAP give a probability distribution over unseen t*?

Question

I'm working my way through the Bayesian world. So far, I've understood that the MLE or the MPA are point estimates, therefore using such models just output one specific value and not a distribution.

Moreover, vanilla neuronal networks do in fact s.th. like MLE, because minimizing the squared-loss or the cross-entropy is similar to finding parameters that maximize the likelihood. Moreover, using neural networks with regularisation is comparable to the MAP estimates, as the prior works like the penalty term in error functions.

However, I've found this work. It shows that the weights $W_{PLS}$ gained from a penalized least-squared are the same as the weights $W_{MAP}$ gained through maximum a posteriori:

However, the paper says:

The first two approaches result in similar predictions, although the MAP Bayesian model does give a probability distribution for $t_*$ The mean of this distribution is the same as that of the classical predictor $y(x_*; W_{PLS})$, since $W_{PLS} = W_{MAP}$

What I don't get here is how can the MAP Bayesian give a proability distribution over $t_*$, when it is only a point estimate?

Consider a neuronal network - a point estimate would mean some fixed weights, so how can there be a output probability distribution? I thought that this is only achieved in the true Bayesian, where we integrate out the unknown weights, therefore building something like the weight averaged of all outcomes, using all possible weights.

Can you help me?

Answer 1

You're correct: the MAP estimate is a point estimate (specifically, MAP is used to estimate the mode of a probability distribution).

I think that the paper is referring to the (output) probability distribution over the possible targets/labels, given the point estimate. However, in the case of MLE, you can also have that probability distribution, so I'm not sure why the paper's author is emphasizing that with MAP you can build that probability distribution (so maybe this/my interpretation of that excerpt is wrong!).

That table also shows that the MAP estimate is used to produce a probability distribution, but the $\sigma$ there should be unknown, but I didn't read that article, so maybe I am missing some info or assumption.

In any case, you could also find a point estimate of a parameter of a probability distribution, but this does not imply that MAP produces a probability distribution. For instance, you can show that, if you place a Gaussian prior on the weights of a neural network, this leads to the $L_2$ loss function, but training a (normal) neural network with $L_2$ does not lead to a probability distribution over the weights.

You should try reading only information from reliable references and books. For MAP, check out chapter 5. (p. 149) of the book "Machine Learning: A Probabilistic Perspective" by Murphy.