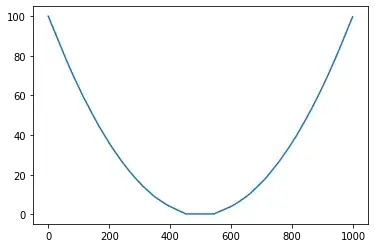
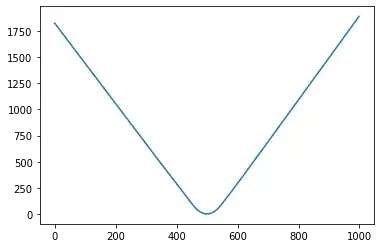
It isn't too surprising to see behaviour like this, since you're using $\mathrm{ReLU}$ activation.
Here is a simple result which explains the phenomenon for a single-layer neural network. I don't have much time so I haven't checked whether this would extend reasonably to multiple layers; I believe it probably will.
Proposition. In a single-layer neural network with $n$ hidden neurons using $\mathrm{ReLU}$ activation, with one input and output node, the output is linear outside of the region $[A, B]$ for some $A < B \in \mathbb{R}$. In other words, if $x > B$, $f(x) = \alpha x + \beta$ for some constants $\alpha$ and $\beta$, and if $x < A$, $f(x) = \gamma x + \delta$ for some constants $\gamma$ and $\delta$.
Proof. I can write the neural network as a function $f \colon \mathbb R \to \mathbb R$, defined by
$$f(x) = \sum_{i = 1}^n \left[\sigma_i\max(0, w_i x + b_i)\right] + c.$$
Note that each neuron switches from being $0$ to a linear function, or vice versa, when $w_i x + b_i = 0$. Define $r_i = -\frac{b_i}{w_i}$. Then, I can set $B = \max_i r_i$ and $A = \min_i r_i$. If $x > B$, each neuron will either be $0$ or linear, so $f$ is just a sum of linear functions, i.e. linear with constant gradient. The same applies if $x < A$.
Hence, $f$ is a linear function with constant gradient if $x < A$ or $x > B$.
$\square$
If the result isn't clear, here's an illustration of the idea:
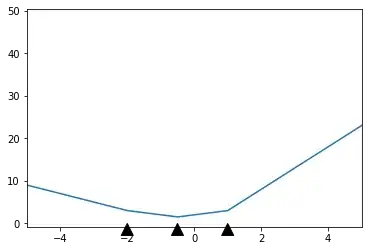
This is a $3$-neuron network, and I've marked the points I denote $r_i$ by the black arrows. Before the first arrow and after the last arrow, the function is just a line with constant gradient: that's what you're seeing, and what the proposition justifies.