I have a relatively small data set comprised of $3300$ data points where each data point is a $13$ dimensional vector where the $12$ first dimensions depict a "category" by taking the form of $[0,...,1,...,0]$ where $1$ is in the $i-th$ position for the $i-th$ category and the last dimension is an observation of a continuous variable, so typically one data point would be $[1,...,0,70.05]$. I'm not trying to have something extremely accurate so I went with a Fully Connected Network with two hidden layers each comprising two neurons, the activation functions are ReLus, one neuron at the output layer because I'm trying to predict one value, and I didn't put any activation function for it. The optimizer is ADAM, the loss is the MSE while the metric is the RMSE.
I get this learning curve below:
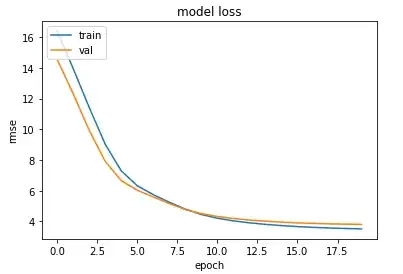 Eventhough at the beginning the validation loss is lesser than the training loss (which I don't understand), I think at the end it show no sign of overfitting.
Eventhough at the beginning the validation loss is lesser than the training loss (which I don't understand), I think at the end it show no sign of overfitting.
What I don't understand is why my Neural Network predicting the same value as long as the $13-th$ dimension takes values greater than $5$ and that value is $0.9747201$. If the $13-th$ dimension takes for example $4.9$ then the prediction would be $1.0005863$. I thought that it has something to do with the ReLu but even when I switched to Sigmoid, I have this "saturation" effect. The value is different but I still get the same value when I pass a certain threshold.
EDIT: I'd also like to add that I get this issue even with normalizing the 13th dimension (substracting the mean and dividing by the standard deviation).
I'd like to add that all the values in my training and validation set are at least greater than $50$ if that may help.