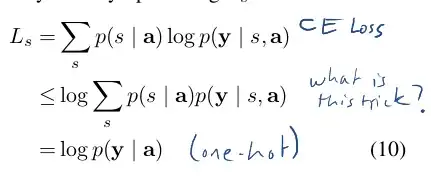How is the jump from line 1 to line 2 done in equation 10 of Show, Attend and Tell?
While we're at it, another thing that might be muddying the waters for me is that I'm not clear on what the sum is over. I know that $s$ is indexed as $s_{t,i}$, but the one-hot trick from line 2 to 3 makes me believe that the sum is over just $i$.
This is Jensen's inequality at work.
First of all, note that the first line can be rewritten as an expectation
$$\sum_{s} p(s \mid \mathbf{a}) \log p(\mathbf{y} \mid s, \mathbf{a}) = \mathbb{E}_{p(s|a)}[\log p(\mathbf{y} \mid s, \mathbf{a})]$$
Then Jensen's inequality gives (Note that a log function is a concave function so gives the opposite inequality to what is normally given when explaining Jensen's inequality with respect to convex functions):
$$\mathbb{E}_{p(s|a)}[\log p(\mathbf{y} \mid s, \mathbf{a})] \leq \log\mathbb{E}_{p(s|a)}[ p(\mathbf{y} \mid s, \mathbf{a})] $$
and then finally you can rewrite the Expectation as a summation.
$$\log\mathbb{E}_{p(s|a)}[ p(\mathbf{y} \mid s, \mathbf{a})] = \log \sum_{s} p(s \mid \mathbf{a}) p(\mathbf{y} \mid s, \mathbf{a})$$
